- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:14.
- Dernière modifié 2025-06-01 06:06.
Vous pourriez penser que les nombres entiers ne sont que des nombres ordinaires, comme 3, -12, 17, 0, 7000 ou -582. Les nombres entiers sont également appelés nombres entiers car ils ne sont pas divisés en parties telles que des fractions et des nombres décimaux. Lisez cet article pour apprendre tout ce dont vous avez besoin sur l'ajout et la soustraction d'entiers, ou lisez directement la section dont vous avez besoin.
Étape
Méthode 1 sur 5: Ajouter et soustraire des nombres entiers positifs à l'aide d'une droite numérique

Étape 1. Comprendre la droite numérique
Les droites numériques transforment les mathématiques de base en quelque chose de tangible et de physique que vous pouvez voir. Avec seulement quelques signes et du bon sens, nous pouvons l'utiliser comme une calculatrice pour additionner et soustraire des nombres.

Étape 2. Tracez une droite numérique de base
Imaginez ou tracez une ligne droite régulière. Faites un point au milieu de votre ligne. Écrivez 0 ou zéro à côté de cette période.
Votre livre de mathématiques pourrait appeler cela le point de départ car c'est le point de départ de tous les nombres

Étape 3. Dessinez deux points, un à droite et à gauche de votre zéro
Écrivez - 1 à côté du point à gauche et
Étape 1. à côté du point à droite. C'est l'entier le plus proche de zéro.
- Ne vous inquiétez pas pour que les distances entre les points soient exactement les mêmes - tant que vous savez ce que signifie chaque point, une droite numérique peut être utilisée.
- Le côté gauche est le début de la phrase.

Étape 4. Complétez votre ligne numérique en ajoutant plus de chiffres
Faites plus de points à gauche que -1 et à droite que 1. A gauche, à partir de -1, marquez vos points avec - 2, - 3, et - 4. Vers la droite, à partir de 1, marquez votre point avec
Étape 2
Étape 3., da
Étape 4.. Vous pouvez continuer si vous avez de la place sur votre papier.
L'exemple de la figure montre une droite numérique de -6 à 6

Étape 5. Comprendre les nombres entiers positifs et négatifs
Entiers positifs, aussi appelés entier naturel, est un entier supérieur à zéro. 1, 2, 3, 25, 99 et 2007 sont des nombres entiers positifs. Les entiers négatifs sont des entiers inférieurs à zéro (comme -2, -4 et -88).
Les nombres entiers sont une autre façon d'appeler des nombres entiers. Les fractions comme 1/2 (la moitié) ne sont qu'une partie du nombre, ce ne sont donc pas des nombres entiers. Identique à la décimale, par exemple 0,25 (zéro virgule deux cinq); décimal n'est pas un entier

Étape 6. Commencez à résoudre 1+2 en plaçant votre doigt sur le point 1
Nous allons résoudre des problèmes d'addition simples 1+2 en utilisant la droite numérique que vous venez de créer. Le premier nombre est
Étape 1., alors commencez à mettre votre doigt sur le numéro.
-
Cette question est-elle trop facile ?
Si vous avez déjà ajouté, vous connaissez probablement la réponse à 1+2. Bien: si vous connaissez le résultat, il sera plus facile de comprendre comment fonctionne la droite numérique. Ensuite, vous pouvez utiliser la droite numérique pour résoudre des problèmes d'addition plus difficiles ou vous préparer à des mathématiques plus difficiles comme l'algèbre.

Étape 7. Additionnez 1+2 en déplaçant votre doigt de 2 points vers la droite
Faites glisser votre doigt vers la droite en comptant le nombre de points (un autre nombre) que vous passez. Si vous avez passé 2 nouveaux points, arrêtez. Le numéro que votre doigt pointe est la réponse,
Étape 3
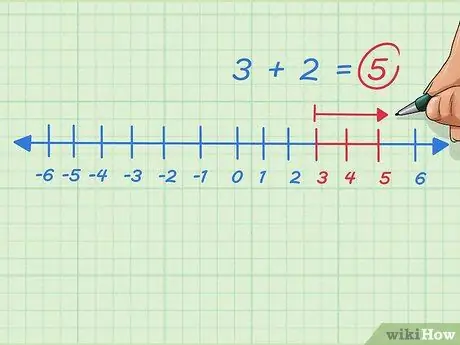
Étape 8. Ajoutez tous les entiers positifs en vous déplaçant vers la droite sur la droite numérique
Supposons que nous voulions résoudre 3+2. Commencez à 3, déplacez-vous vers la droite ou ajoutez 2 points. On s'arrête à 5. Le problème s'écrit 3 + 2 = 5.

Étape 9. Soustrayez les nombres entiers positifs en vous déplaçant vers la gauche sur la droite numérique
Par exemple, on veut résoudre 6 -4, on commence à 6, on se déplace vers la gauche de 4 points, et on s'arrête à 2. Ce problème s'écrit 6 - 4 = 2.
Méthode 2 sur 5: Ajouter et soustraire des nombres négatifs à l'aide d'une droite numérique

Étape 1. En savoir plus sur les droites numériques
Si vous ne savez pas comment créer une droite numérique, revenez à la section Addition et soustraction de nombres positifs à l'aide de droites numériques pour apprendre à en créer une.
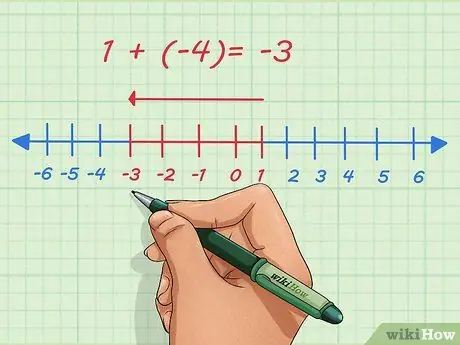
Étape 2. Comprendre les nombres négatifs
Les nombres positifs sont indiqués par la direction vers la droite sur la droite numérique. Les nombres négatifs sont indiqués à gauche sur la droite numérique. Ajouter des nombres négatifs signifie déplacer le point vers la gauche sur la droite numérique.
-
Par exemple, ajoutons 1 et -4. Habituellement, cette question s'écrit comme ceci:
1 + (-4)
. Sur la droite numérique, on commence à 1, on se déplace de 4 points vers la gauche et on s'arrête à -3.
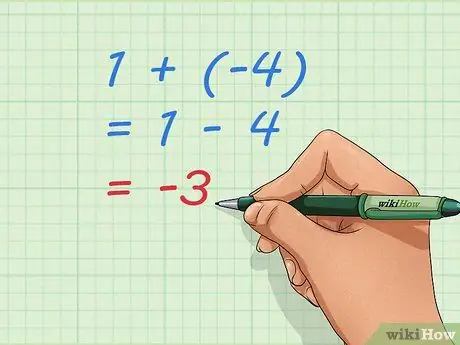
Étape 3. Utilisez des équations de base pour comprendre l'addition de nombres négatifs
Notez que -3, notre réponse, est le nombre que nous obtiendrons si nous faisons 1 - 4. Ajouter 1 + (-4) et soustraire 4 de 1 est le même problème. Nous pouvons l'écrire comme une équation, une phrase mathématique qui montre l'égalité:1 + (-4) = 1 - 4 = -3
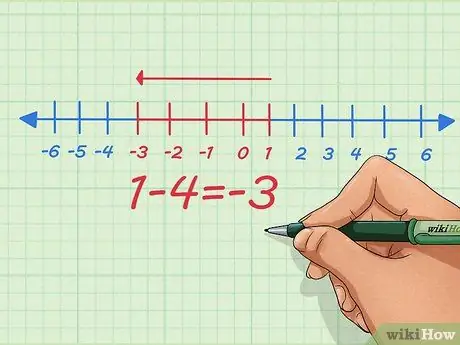
Étape 4. Au lieu d'ajouter des nombres négatifs, transformez-le en un problème de soustraction en utilisant des nombres positifs
Comme nous pouvons le voir à partir de l'équation simple ci-dessus, nous pouvons faire les deux - transformer l'addition de nombres négatifs en soustraction de nombres positifs et vice versa. On vous a peut-être appris à transformer les négatifs en négatifs sans savoir pourquoi - voici pourquoi.
-
Par exemple, -4. Quand on additionne -4 et 1, on soustrait 1 par 4. On peut l'écrire en maths en écrivant
1 + (-4) = 1 - 4
. Nous pouvons l'écrire sur la droite numérique, en commençant par notre point de départ à 1, puis en ajoutant 4 points vers la gauche (en d'autres termes, en ajoutant -4). Puisqu'il s'agit d'une équation, une chose est égale à une autre - donc l'inverse est également vrai
1 - 4 = 1 + (-4)
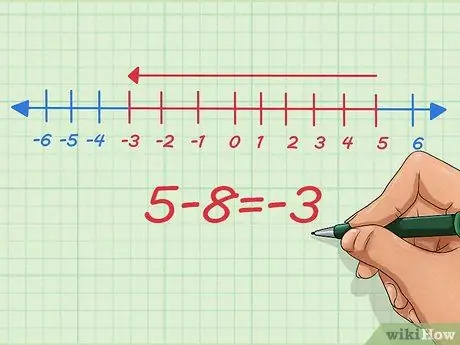
Étape 5. Comprendre comment soustraire des nombres négatifs sur une droite numérique
Sur la droite numérique, soustraire des nombres négatifs revient à réduire la longueur. Commençons par 5 - 8.
Sur la droite numérique, nous commençons à notre point de départ à 5, soustrayons 8 et arrêtons à -3
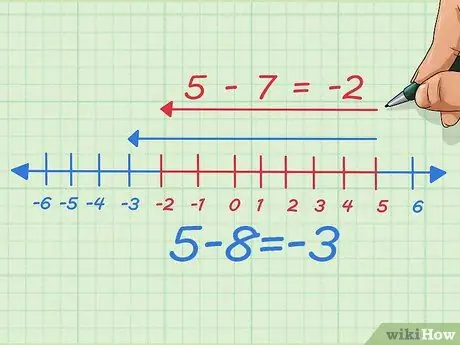
Étape 6. Soustrayez le montant que vous soustrayez et voyez ce qui se passe
Supposons que nous soustrayons un, le nombre que nous soustrayons, ou en d'autres termes soustrayons 7 au lieu de 8. Maintenant, nous soustrayons un point vers la gauche sur la droite numérique. A l'écriture, on a commencé avec 5 - 8 = -3 Maintenant, on déplace juste 7 vers la gauche, donc ça devient 5 - 7 = -2
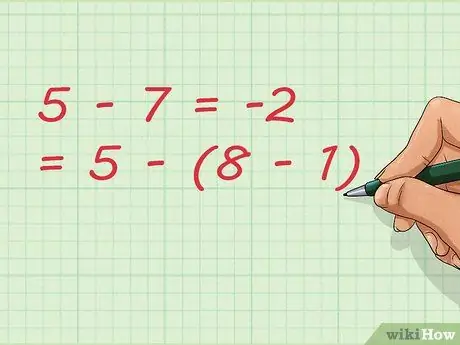
Étape 7. Notez que la soustraction peut entraîner une addition
Dans notre exemple, nous soustrayons le nombre 1. En écrivant l'équation, nous pouvons l'écrire plus court comme: 5 - 7 = -2 = 5 - (8 - 1)

Étape 8. Convertissez les signes négatifs en positifs lors de l'ajout de nombres négatifs
En utilisant l'étape de conversion de toutes les soustractions en additions, nous pouvons écrire des plus courtes comme: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Nous savons déjà que 5 - 8 = -3, alors retirez 5 - 8 de l'équation et entrez -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Nous savons déjà que 5 - (8 - 1) est - soustrait un point de 5 - 8. Notre équation peut montrer que 5 - 8 est égal à -3, et la soustraction d'un point donne -2. L'équation peut s'écrire ainsi:
-3 - (-1) = -3 + 1
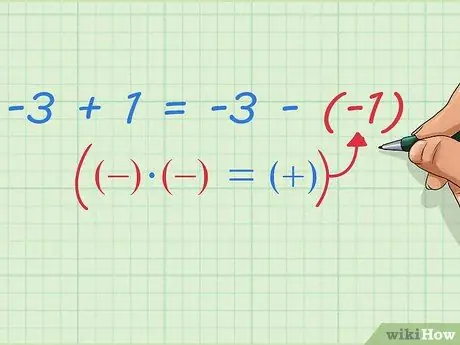
Étape 9. Écrivez la soustraction de nombres négatifs sous forme d'addition
Remarquez ce qui se passe après cela - nous avons déjà prouvé que: -3 + 1 = -3 - (-1) Nous pouvons écrire ceci avec des règles d'écriture mathématique plus simples et plus générales: premier nombre plus deuxième nombre = premier nombre moins (deuxième nombre négatif) Ou, une manière plus simple que vous avez probablement entendue en cours de mathématiques: Changer les deux signes négatifs en un signe positif.
Méthode 3 sur 5: Ajout de grands entiers positifs

Étape 1. Écrivez le problème d'addition de 2 503 + 7 461 avec un nombre sur l'autre
Écrivez les nombres dans la grande colonne de sorte que 2 soit supérieur à 7, 5 soit supérieur à 4, et ainsi de suite. De cette façon, nous apprendrons à additionner des nombres entiers trop grands pour imaginer ou utiliser la droite numérique.
Écrivez un signe + à gauche du nombre ci-dessous et de la ligne en dessous, comme vous pourriez l'apprendre pour des problèmes d'addition plus petits
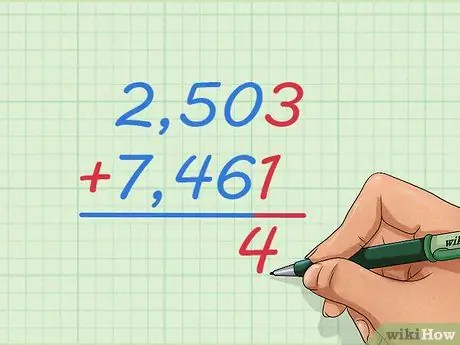
Étape 2. Commencez par additionner les deux nombres à l'extrême droite
Cela peut être un peu étrange de commencer par la droite parce que nous lisons les nombres à partir de la gauche. Nous devons ajouter à partir de la droite pour obtenir la bonne réponse, que vous pourrez voir plus tard.
-
Sous les deux chiffres les plus à droite,
Étape 3. da
Étape 1., notez la somme des deux
Étape 4..

Étape 3. Additionnez chaque nombre de la colonne de la même manière
Déplacer vers la gauche, additionner 0+6, 5+4, et 2+7. Écrivez la réponse sous chaque paire de nombres.
Votre réponse devrait être: 9.964. Vérifiez votre travail si vous faites une erreur.

Étape 4. Ajoutez maintenant 857+135
Vous remarquerez quelque chose de différent dès que vous additionnez la première paire de nombres à droite. 7+5 est égal à 12, un nombre à deux chiffres, mais vous ne pouvez écrire qu'un chiffre dans cette colonne. Continuez votre lecture pour savoir ce que vous devez faire et pourquoi vous devez toujours commencer par la droite et non par la gauche.

Étape 5. Additionnez 7+5 et apprenez où écrire la réponse
7+5=12, mais vous ne pouvez pas mettre 1 et 2 sous la ligne. Mais, écrivez le dernier chiffre, Étape 2., sous la ligne et notez le premier chiffre
Étape 1., au-dessus de la colonne de gauche, 5+3.
-
Si vous êtes curieux de savoir comment cela fonctionne, pensez à ce que signifie diviser 1 et 2. Vous divisez en fait 12 en
Étape 10. da
Étape 2.. Vous pouvez écrire 10 au-dessus du nombre si vous le souhaitez, et vous verrez 1 dans les colonnes 5 et 3, comme avant.

Étape 6. Additionnez 1+5+3 pour obtenir le chiffre suivant de la réponse
Vous avez maintenant trois chiffres à additionner car vous avez ajouté 1 à cette colonne. La réponse est
Étape 9., donc votre réponse devient 92.
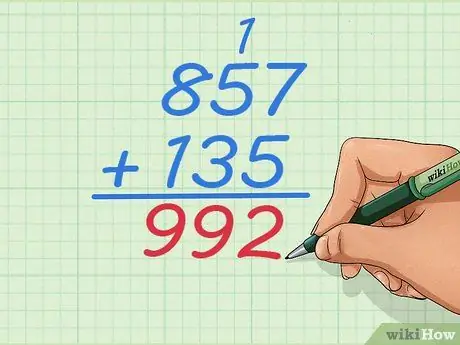
Étape 7. Terminez le problème comme d'habitude
Continuez à travailler les chiffres vers la gauche jusqu'à ce que vous ayez additionné tous les nombres, dans ce cas, il ne reste qu'une colonne. Votre réponse finale devrait être 992.
- Vous pouvez essayer des questions plus compliquées, comme 974+568. N'oubliez pas que chaque fois que vous obtenez un nombre à deux chiffres, n'écrivez que le dernier chiffre comme réponse et placez l'autre chiffre au-dessus de la colonne de gauche, que vous additionnerez ensuite. Si la réponse dans la dernière colonne (à l'extrême gauche) contient deux chiffres, notez-la comme votre réponse.
- Consultez la section Astuces pour obtenir des réponses aux questions 974+568 une fois que vous avez essayé de les résoudre.
Méthode 4 sur 5: Soustraction de grands entiers positifs

Étape 1. Écrivez le problème de soustraction 4,713 - 502 avec le premier nombre au-dessus du deuxième nombre
Écrivez-le de sorte que 3 soit directement au-dessus de 2, 1 au-dessus de 0, 7 au-dessus de 5 et 4 au-dessus du blanc.
Vous pouvez écrire 0 sous 4 si cela vous aide à vous rappeler quel nombre est au-dessus de quel nombre. Vous pouvez toujours ajouter un 0 devant un nombre sans le changer. Assurez-vous de l'ajouter avant le numéro, pas après

Étape 2. Soustrayez chaque nombre ci-dessous du nombre directement au-dessus
Commencez toujours par la droite. Résolvez 3-2, 1-0, 7-5 et 4-0, écrivez la réponse à chaque question directement sous les deux nombres soustraits.
Le résultat est, 4.211.

Étape 3. Rédigez maintenant les questions 924 à 518 de la même manière
Ces nombres ont le même nombre de chiffres, vous pouvez donc les écrire facilement. Ce problème vous apprendra quelque chose sur la soustraction d'entiers si vous ne le savez pas déjà.

Étape 4. Apprenez à résoudre le premier problème, qui se trouve à l'extrême droite
4 - 8. Ce problème est compliqué car 4 est inférieur à 8, mais n'utilisez pas de nombres négatifs, mais suivez ces étapes:
- Dans la rangée du haut, croisez 2 et écrivez 1. 2 devrait être à gauche de 4.
- Croisez 4 et écrivez 14. Faites ceci dans un espace étroit pour qu'il soit clair que 14 est supérieur à 8. Vous pouvez également écrire 1 devant 4 pour faire 14 s'il y a suffisamment d'espace.
- Ce que vous venez de faire est d'emprunter 1 à la place des dizaines ou de la deuxième colonne à droite et de le convertir en 10 à la place des unités ou à la colonne la plus à droite. Une fois que le nombre 10 est égal à dix fois le nombre 1, c'est donc pareil.

Étape 5. Résolvez maintenant les problèmes 14 à 8 et écrivez la réponse dans la colonne la plus à droite
Il aurait dû écrire 6 sur la ligne de réponse la plus à droite.

Étape 6. Complétez la colonne suivante à gauche, en utilisant le nouveau numéro que vous avez noté
La soustraction doit être de 1 à 1, ce qui est égal à 0.
Votre réponse devrait maintenant être 06.

Étape 7. Résolvez le problème en complétant la dernière soustraction, la colonne la plus à gauche
9 - 5 = 4, donc votre réponse finale est 406.

Étape 8. Nous résolvons maintenant le problème de la soustraction de grands nombres à de petits nombres
Supposons qu'on vous demande de remplir 415 990 - 968 772. Écrivez le deuxième nombre sous le premier et vous vous rendrez compte que le nombre ci-dessous est plus gros ! Vous pouvez le voir immédiatement à partir du premier chiffre à gauche: 9 est supérieur à 4, donc les nombres commençant par 9 sont plus gros.
Assurez-vous d'écrire correctement la colonne avant de comparer. 912 non supérieur à 5000, vous pouvez savoir si vous écrivez correctement la colonne car il n'y a pas de nombres inférieurs à 5. Vous pouvez ajouter zéro aide, par exemple, écrivez 912 avec 0912 pour que la colonne soit égale à 5000.

Étape 9. Écrivez le plus petit nombre sous le plus grand nombre et ajoutez un signe - devant la réponse
Chaque fois que vous soustrayez un nombre à un nombre plus petit, le résultat est un nombre négatif. Il est préférable d'écrire ce signe avant de soustraire afin de ne pas oublier de l'écrire.

Étape 10. Pour répondre, soustrayez le petit nombre du grand nombre et n'oubliez pas d'écrire le signe -
Votre réponse sera négative, ce qui est indiqué par un signe -. Ne pas essaie de soustraire un grand nombre d'un petit nombre, puis rend le résultat négatif; votre réponse sera fausse.
Le nouveau problème à résoudre est: 968 772 - 415 990 = -? Voir la section Conseils pour la réponse après avoir essayé de résoudre ce problème
Méthode 5 sur 5: Ajout et soustraction d'entiers négatifs
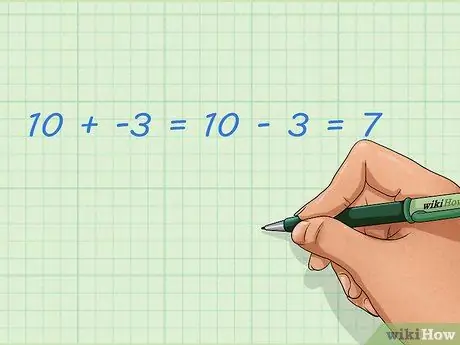
Étape 1. Apprenez à ajouter des nombres négatifs et positifs
Ajouter des entiers négatifs revient à soustraire des entiers positifs. C'est plus facile à faire avec la droite numérique décrite dans une autre section, mais vous pouvez aussi y penser avec des mots. Les nombres négatifs ne sont pas des nombres ordinaires; ce nombre est inférieur à zéro et peut représenter le montant prélevé. Si vous ajoutez cette prise à un nombre normal, le résultat devient plus petit.
- Exemple: 10 + -3 = 10 - 3 = 7
- Exemple: -12 + 18 = 18 + -12 = 18 - 12 = 6. N'oubliez pas que vous pouvez toujours modifier l'ordre des nombres en plus, mais pas en soustraction.
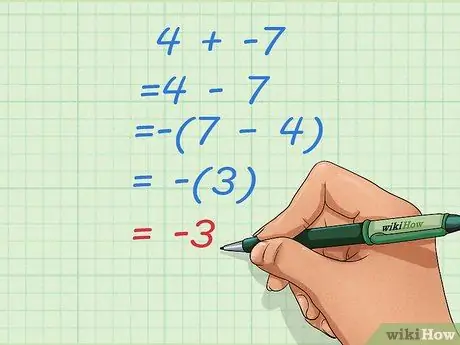
Étape 2. Apprenez ce que vous devez faire si vous le transformez en un problème de soustraction avec un nombre de départ plus petit
Parfois, changer des problèmes d'addition en soustraction comme celui ci-dessus peut conduire à des réponses étranges comme 4 à 7. Lorsque cela se produit, inversez l'ordre des nombres et rendez votre résultat négatif.
- Disons que votre problème initial est 4 + -7.
- Transformez-le en un problème de soustraction: 4 - 7
- Inversez l'ordre et rendez le résultat négatif: -(7 - 4) = -(3) = -3.
- Si vous n'êtes pas habitué à utiliser des parenthèses dans les équations, pensez à ceci: 4 - 7 se transforme en 7 - 4 avec l'ajout d'un signe négatif. 7 - 4 = 3, mais nous devons le changer en -3 pour que la réponse aux questions 4 - 7 soit correcte.
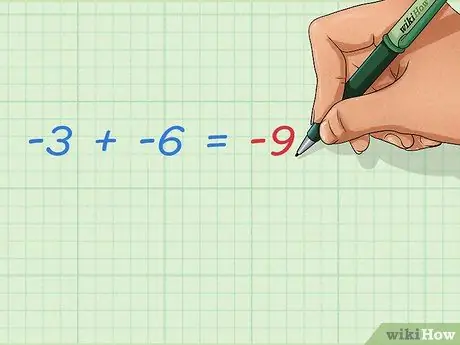
Étape 3. Apprenez à additionner deux nombres entiers négatifs
Deux nombres négatifs ajoutés augmentent toujours le résultat négatif. Comme aucun nombre positif n'est ajouté, le résultat sera plus éloigné de 0. La réponse est simple:
- -3 + -6 = -9
- -15 + -5 = -20
- Voyez-vous le motif? Tout ce que vous avez à faire est d'additionner les nombres comme s'il s'agissait de nombres positifs et d'ajouter un signe négatif. -4 + -3 = -(4 + 3) = -7
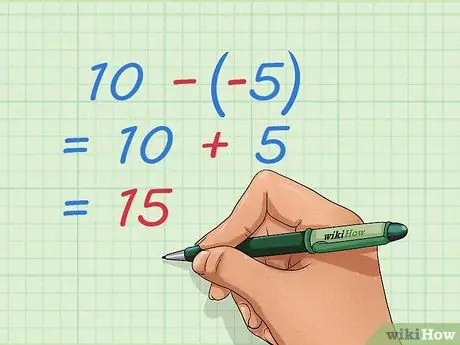
Étape 4. Apprenez à soustraire des nombres entiers négatifs
Comme le problème d'addition, vous pouvez réécrire le problème de manière à n'avoir que des nombres positifs. Si vous soustrayez des nombres négatifs, vous enlevez certaines des choses qui ont déjà été prises, ce qui revient à ajouter des nombres positifs.
- Considérez les nombres négatifs comme de l'argent volé. Si vous soustrayez ou retirez de l'argent volé pour pouvoir le rendre, c'est comme donner de l'argent à quelqu'un, n'est-ce pas ?
- Exemple: 10 - -5 = 10 + 5 = 15
- Exemple: -1 - -2 = -1 + 2. Vous avez déjà appris à résoudre ce problème lors de la première étape, vous vous souvenez ? Relisez comment ajouter des nombres négatifs et positifs si vous avez oublié.
- Voici la solution complète du dernier exemple: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Des astuces
- Vous avez peut-être écrit des nombres longs comme 2 521 301 en utilisant des virgules (,) au lieu de (.) selon votre lieu de résidence. Utilisez ce que votre professeur vous demande pour ne pas vous tromper avec d'autres systèmes d'écriture.
- Dessinez vos droites numériques sur différentes échelles pour représenter différents nombres. Il n'y a pas de règle selon laquelle chaque distance sur une droite numérique est égale à 1. Imaginez une droite numérique qui vaut 10 au lieu de 1. Mis à part le fait que chaque point vaut 10 maintenant, l'addition et la soustraction restent les mêmes. Essayez-le si vous n'y croyez pas.
- Si vous essayez les questions de défi spéciales dans la section Nombres longs, voici la réponse: 974 + 568 = 1.542. La réponse de 415 990 à 968 772 est - 552.782.






