Diviser des fractions par des nombres entiers n'est pas aussi difficile qu'il y paraît. Pour diviser une fraction par un entier, il suffit de convertir le nombre entier en fraction, de trouver l'inverse de la fraction et de multiplier le résultat par la première fraction. Si vous voulez savoir comment le faire, suivez simplement ces étapes:
Étape
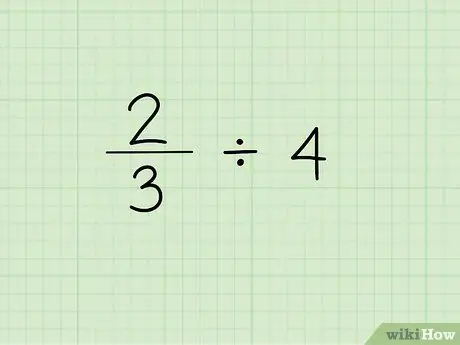
Étape 1. Notez le problème
La première étape pour diviser une fraction par un entier consiste à écrire la fraction suivie du signe de division et de l'entier dont vous avez besoin pour diviser la fraction. Disons que nous travaillons avec le problème suivant: 2/3 4.
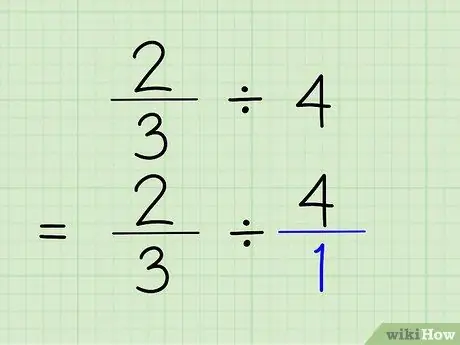
Étape 2. Convertissez des nombres entiers en fractions
Pour convertir un entier en fraction, il suffit de placer l'entier au dessus du chiffre 1. L'entier devient le numérateur et 1 devient le dénominateur de la fraction. Dire 4/1 revient vraiment à dire 4, car vous ne montrez que le nombre contient "1" 4 fois. Le problème sera 2/3 4/1.
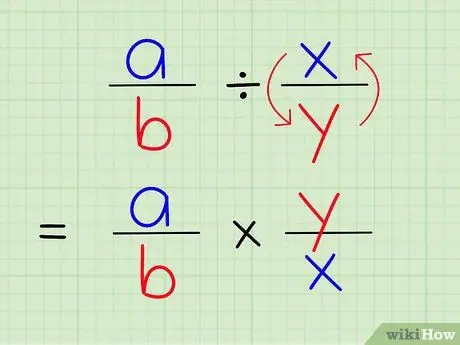
Étape 3. Diviser une fraction par une autre revient à multiplier cette fraction par l'inverse d'une autre fraction
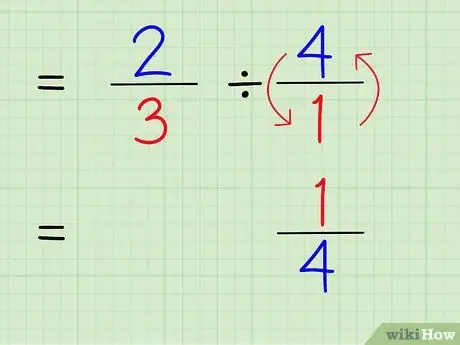
Étape 4. Écrivez l'inverse de l'entier
Pour trouver l'inverse d'un nombre, échangez le numérateur et le dénominateur du nombre. Par conséquent, pour trouver l'inverse de 4/1, il suffit d'intervertir le numérateur et le dénominateur pour que le nombre devienne 1/4.
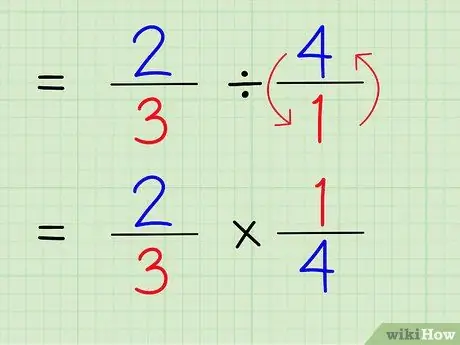
Étape 5. Remplacez le signe de division par le signe de multiplication
Le problème sera 2/3 x 1/4.
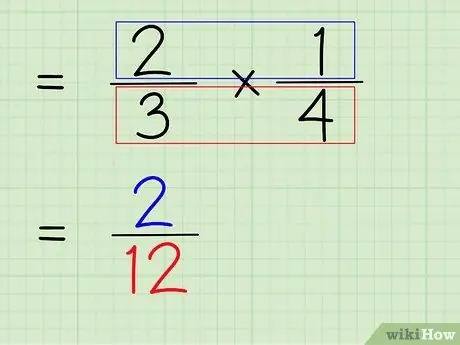
Étape 6. Multipliez le numérateur et le dénominateur de la fraction
Ainsi, l'étape suivante consiste à multiplier le numérateur et le dénominateur de la fraction pour obtenir un nouveau numérateur et dénominateur comme réponse finale.
- Pour multiplier les numérateurs, il suffit de multiplier 2 x 1 pour obtenir 2.
- Pour multiplier les dénominateurs, il suffit de multiplier 3 x 4 pour obtenir 12.
- 2/3 x 1/4 = 2/12
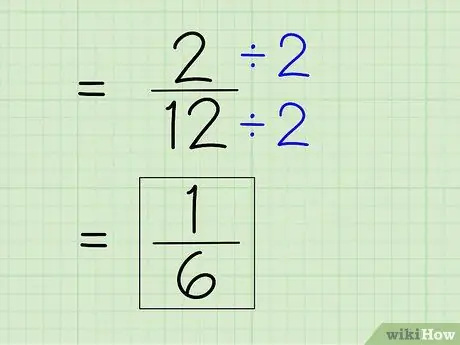
Étape 7. Simplifiez la fraction
Pour simplifier une fraction, vous devez trouver le plus petit dénominateur, ce qui signifie que vous devez diviser le numérateur et le dénominateur par n'importe quel nombre qui divise les deux nombres. Puisque 2 est le numérateur, vous devrez voir si 2 peut diviser 12 complètement -- c'est possible parce que 12 est un nombre pair. Ensuite, divisez le numérateur et le dénominateur par 2 pour obtenir un nouveau numérateur et un nouveau dénominateur pour obtenir une réponse simple.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- La fraction 2/12 peut être simplifiée en 1/6. Ceci est votre réponse finale.
Des astuces
- C'est pour aider la mémoire, un moyen facile de se rappeler comment faire tous ces calculs. Gardez ceci à l'esprit: « C'est facile de diviser des fractions, d'inverser le deuxième nombre et de multiplier ! »
- Une autre variante de la méthode ci-dessus est JGB/JBG. Ne changez pas le premier numéro. Passez à la multiplication. Inversez le dernier chiffre. Ou B d'abord puis G.
- Si vous annulez le calcul avant de le multiplier, vous n'aurez peut-être pas besoin de trouver la forme la plus simple de la fraction car le résultat est déjà sous la forme la plus simple de la fraction, comme vous pouvez le voir. Dans notre exemple, avant de multiplier 2/3 × 1/4, nous pouvons voir que le premier numérateur (2) et le deuxième dénominateur (4) ont le même multiplicateur de 2, que nous pouvons annuler avant de continuer le calcul. Cela convertit le problème en 1/3 × 1/2, ce qui donne un résultat immédiat de 1/6 et nous fait gagner du temps en simplifiant la fraction à un stade ultérieur.
- Si l'une de vos fractions est négative, cette méthode est toujours utilisable; assurez-vous de garder une trace des signes pendant que vous effectuez ces étapes.
