- Auteur Jason Gerald [email protected].
- Public 2024-01-15 08:14.
- Dernière modifié 2025-01-23 12:18.
Diviser une fraction par une fraction peut sembler déroutant au début, mais c'est en fait très facile. Il ne vous reste plus qu'à retourner, multiplier et simplifier ! Cet article vous guidera tout au long du processus et vous montrera à quel point il est facile de diviser une fraction par une fraction.
Étape
Partie 1 sur 2: Comprendre comment diviser des fractions par des fractions
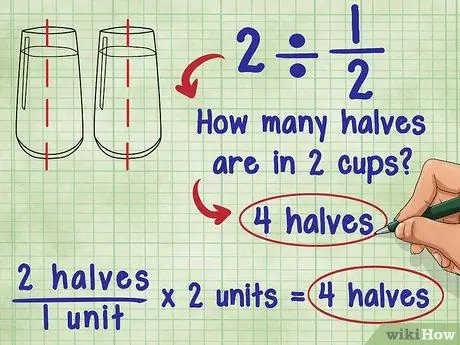
Étape 1. Réfléchissez à ce que signifie diviser par une fraction
Sur 2 ÷ 1/2 demanda Ada: « Combien y a-t-il de moitiés dans 2 ? La réponse est 4 car chaque unité (1) se compose de deux « demi », et il y a 2 unités au total: 2 « demi »/1 unité * 2 unités = 4 « demi ».
- Essayez d'imaginer la même équation en utilisant un verre d'eau: Combien y a-t-il de verres et demi d'eau dans 2 verres d'eau ? Vous pouvez verser 2 tasses et demie d'eau dans chaque verre d'eau. Cela signifie, en gros, que vous additionnez les "demi" verres d'eau, et vous avez deux verres: 2 "demi"/1 tasse * 2 tasses = 4 "demi".
- Cela signifie que si la fraction que vous divisez est comprise entre 0 et 1, la réponse est toujours supérieure au nombre d'origine ! Cela est vrai lorsque vous divisez un nombre entier ou une fraction par une fraction.

Étape 2. Comprenez que la division est le contraire de la multiplication
Ainsi, la division par une fraction peut être résolue en multipliant par l'inverse de la fraction. L'inverse d'une fraction (également appelé « inverse de multiplication ») est la fraction qui est inversée, de sorte que le numérateur et le dénominateur s'intervertissent. Dans un instant, nous allons diviser des fractions par des fractions, en trouvant l'inverse de la deuxième fraction et en multipliant les deux fractions. Cependant, examinons d'abord quelques-uns des contraires:
- L'inverse de 3/4 est 4/3.
- Le contraire de 7/5 est 5/7.
- L'inverse de 1/2 est 2/1 ou 2.
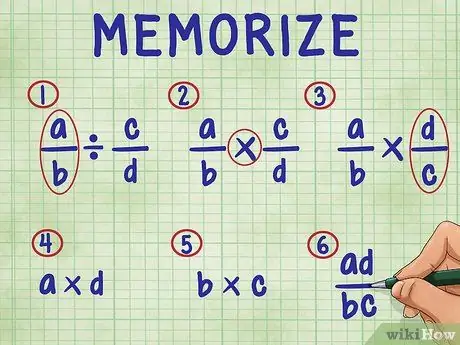
Étape 3. N'oubliez pas les étapes suivantes pour diviser une fraction par une fraction
Dans l'ordre, les étapes comprennent:
- Laissez simplement la première fraction de l'équation.
- Remplacez le signe de division par le signe de multiplication.
- Inverser la seconde fraction (trouver son inverse).
- Multipliez le numérateur (numéro du haut) des deux fractions. Le résultat de la multiplication est le numérateur (en haut) de votre réponse.
- Multipliez le dénominateur (nombre du bas) des deux fractions. Le produit du produit est le dénominateur de votre réponse.
- Simplifiez vos fractions en les simplifiant dans leurs termes les plus simples.
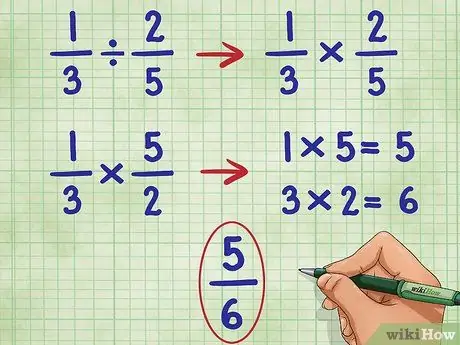
Étape 4. Effectuez ces étapes pour l'exemple 1/3 2/5
Nous commencerons par omettre la première fraction et par convertir le signe de division en signe de multiplication:
- 1/3 ÷ 2/5 = Devient:
- 1/3 * _ =
- Maintenant, nous renversons la deuxième fraction (2/5) pour trouver sa réciproque, qui est 5/2:
- 1/3 * 5/2 =
- Maintenant, multipliez le numérateur (numéro du haut) des deux fractions, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Maintenant, multipliez le dénominateur (nombre du bas) des deux fractions, 3*2 = 6.
- Maintenant nous avons: 1/3 * 5/2 = 5/6
- Cette fraction ne peut pas être simplifiée davantage, nous avons donc notre réponse.

Étape 5. Essayez de vous rappeler les comptines suivantes pour vous aider à vous en souvenir:
"Il est facile de diviser des fractions, inversez la deuxième fraction, puis multipliez. N'oubliez pas de simplifier, avant qu'il ne soit temps de manger."
Un autre aide-mémoire utile vous indique quoi faire avec chaque partie de l'équation: « Laissez-moi (première fraction), Changez-moi (signe de division), Inversez-moi (deuxième fraction). »
Partie 2 sur 2: Diviser les fractions par les fractions dans les problèmes
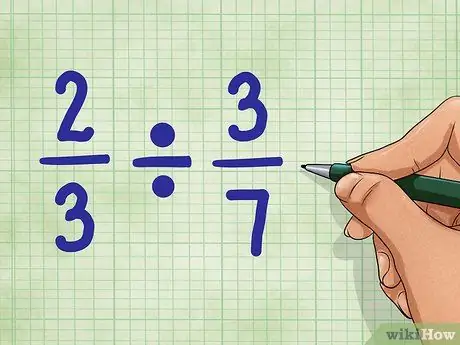
Étape 1. Commencez par des exemples de questions
utilisons 2/3 ÷ 3/7. Cette question demande le nombre de pièces égal à 3/7, que l'on retrouve dans la valeur 2/3. Ne t'inquiète pas. Ce n'est pas aussi difficile qu'il y paraît !
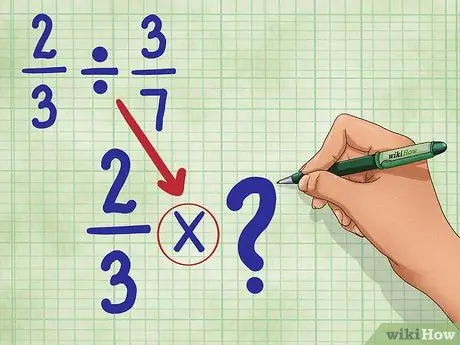
Étape 2. Convertissez le signe de division en signe de multiplication
Votre nouvelle équation sera: 2/3 * _ (Nous allons remplir ce vide dans un instant.)
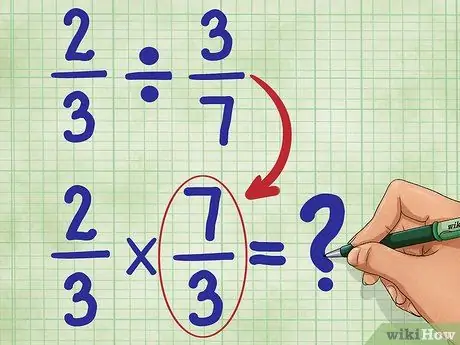
Étape 3. Maintenant, trouvez l'inverse de la deuxième fraction
Cela signifie retourner 3/7 pour que le numérateur (3) soit maintenant en bas et que le dénominateur (7) soit maintenant en haut. L'inverse de 3/7 est 7/3. Maintenant, écrivez votre nouvelle équation:
2/3 * 7/3 = _

Étape 4. Multipliez vos fractions
Tout d'abord, multipliez les numérateurs des deux fractions: 2 * 7 = 14. 14 est le numérateur (numéro du haut) de votre réponse. Ensuite, multipliez les dénominateurs des deux fractions: 3 * 3 = 9. 9 est le dénominateur (numéro du bas) de votre réponse. Maintenant, tu sais que 2/3 * 7/3 = 14/9.
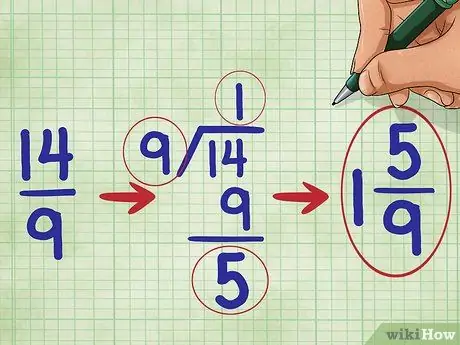
Étape 5. Simplifiez votre fraction
Dans ce problème, parce que le numérateur de la fraction est supérieur au dénominateur, nous savons que notre fraction est supérieure à 1. Nous devons la convertir en un nombre mixte. (Un nombre mixte est un nombre entier et une fraction combinés, par exemple 1 2/3.))
-
Divisez d'abord le numérateur
Étape 14. avec 9.
Le nombre 14 divisé par 9 est égal à un avec un reste de 5, vous devez donc écrire votre fraction simplifiée comme suit: 1 5/9 (« un cinq-neuvième »).
- Arrêtez, vous avez trouvé la réponse ! Vous pouvez spécifier que vous ne pouvez plus simplifier la fraction car le dénominateur n'est pas divisible par le numérateur (9 n'est pas divisible par 5) et le numérateur est un nombre premier, ou un entier qui n'est divisible que par un et le nombre lui-même.
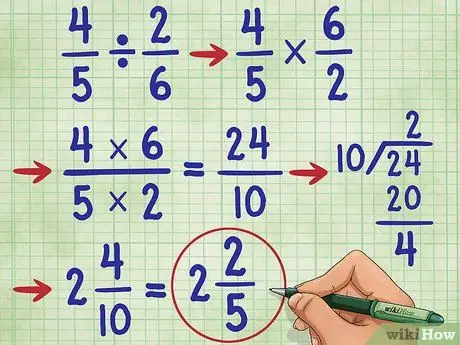
Étape 6. Essayez un autre exemple
Essayons la question 4/5 ÷ 2/6 =. Tout d'abord, remplacez le signe de division par le signe de multiplication (4/5 * _ =), puis trouvez l'inverse de 2/6, qui est 6/2. Maintenant, vous avez l'équation: 4/5 * 6/2 =_. Maintenant, multipliez le numérateur, 4 * 6 = 24, et le dénominateur 5* 2 = 10. Maintenant vous avez 4/5 * 6/2 = 24/10.
Maintenant, simplifiez la fraction. Puisque le numérateur est supérieur au dénominateur, nous devons convertir cette fraction en un nombre fractionnaire.
- Tout d'abord, divisez le numérateur par le dénominateur, (24/10 = 2 restants 4).
- Écrivez la réponse comme 2 4/10. On peut encore simplifier cette fraction à nouveau !
- Notez que 4 et 10 sont des nombres pairs. Ainsi, la première étape pour le simplifier est de diviser chaque nombre par 2. Nous obtenons 2/5.
- Puisque le dénominateur (5) n'est pas divisible par le numérateur (2) et que 5 est un nombre premier, nous savons que cette fraction ne peut plus être simplifiée. Alors, notre réponse est: 2 2/5.

Étape 7. Obtenez de l'aide supplémentaire pour simplifier les fractions
Vous avez probablement passé beaucoup de temps à apprendre à simplifier des fractions avant d'essayer de les diviser les unes par les autres. Cependant, si vous avez besoin d'un rappel ou d'une autre aide, il existe d'excellents articles en ligne qui peuvent vous être d'une grande utilité.
Articles wikiHow connexes
- Conversion de fractions communes en décimales
- Calcul de l'aire d'un cercle
- Division de polynômes à l'aide de la division synthétique
- Division de fractions mixtes






