- Auteur Jason Gerald [email protected].
- Public 2024-01-15 08:14.
- Dernière modifié 2025-06-01 06:06.
Diviser par des nombres décimaux semble difficile au début car personne ne vous a appris la « table de 0, 7 fois ». Le secret pour cela est de convertir le problème de division dans un format qui n'utilise que des nombres entiers. Après avoir réécrit le problème de cette manière, il deviendra un problème régulier de longue division.
Étape
Partie 1 sur 2: Problèmes d'écriture en tant que problèmes de division ordinaire
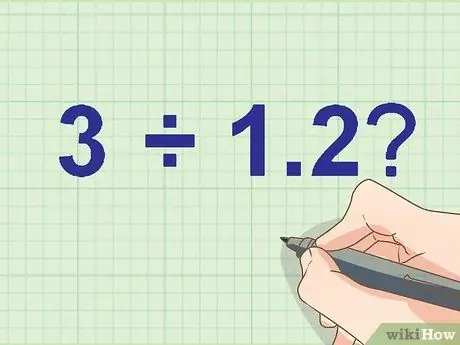
Étape 1. Écrivez votre problème de division
Utilisez un crayon si vous voulez améliorer votre travail.
-
Exemple:
Combien de 3 ÷ 1, 2?

Étape 2. Écrivez le nombre entier sous forme décimale
Écrivez une virgule après le nombre entier, puis écrivez un zéro après la virgule. Faites-le jusqu'à ce que les deux nombres aient la même valeur de position à droite de la virgule décimale. Cela ne change pas la valeur entière.
-
Exemple:
Dans le problème 3 1, 2, notre nombre entier est 3. Puisque 1, 2 a une valeur de position à droite de la virgule décimale, écrivez 3 comme 3, 0 afin que ce nombre ait également une valeur de position après la virgule. Maintenant, notre affaire devient 3, 0 ÷ 1, 2.
- Attention: n'ajoutez pas de zéros à gauche de la virgule décimale ! Le nombre 3 est égal à 3, 0 ou 3, 00, mais pas égal à 30 ou 300.

Étape 3. Déplacez la virgule vers la droite jusqu'à ce que vous obteniez un nombre entier
Dans les problèmes de division, vous pouvez déplacer les points décimaux, mais seulement si vous déplacez les points décimaux sur tous les nombres du même nombre de pas. Cela vous permet de convertir le problème en un nombre entier.
-
Exemple:
Pour convertir 3, 0 1, 2 en un nombre entier, déplacez le point décimal d'un cran vers la droite. Ainsi, 3, 0 devient 30 et 1, 2 devient 12. Maintenant, notre problème devient 30 ÷ 12.

Étape 4. Écrivez le problème en utilisant la division longue
Placez le nombre divisible (généralement le plus grand nombre) sous le symbole de division longue. Écrivez le numéro du diviseur à l'extérieur de ce symbole. Maintenant, vous avez un problème de division longue régulier qui utilise des nombres entiers. Si vous voulez un rappel sur la façon de faire une division longue, lisez la section suivante.
Partie 2 sur 2: Résoudre les problèmes de division longue

Étape 1. Trouvez le premier chiffre de la réponse
Commencez à résoudre ce problème de la même manière que vous le feriez normalement, en comparant le diviseur et le premier chiffre du nombre divisé. Calculez le résultat de la division de ce premier chiffre par le nombre du diviseur, puis écrivez le résultat au-dessus de ce chiffre.
Exemple: Nous essayons de diviser 30 par 12. Comparez 12 avec le premier chiffre du nombre divisé, qui est 3. Puisque 12 est supérieur à 3, 3 divisé par 12 est égal à 0. Notez 0 au-dessus de 3 dans la ligne de réponse.
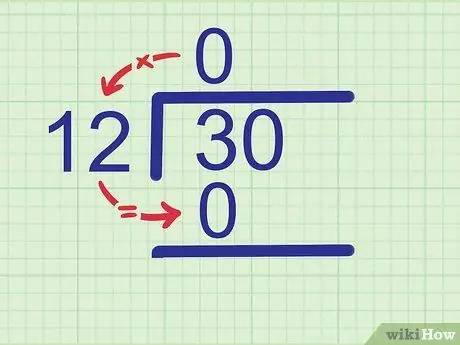
Étape 2. Multipliez le quotient par le diviseur
Écrivez le produit du produit sous le nombre qui est divisé. Écrivez le résultat juste en dessous du premier chiffre du nombre que vous avez divisé car c'est le chiffre que vous venez de voir.
-
Exemple:
Puisque 0 x 12 = 0, écrivez 0 moins de 3.
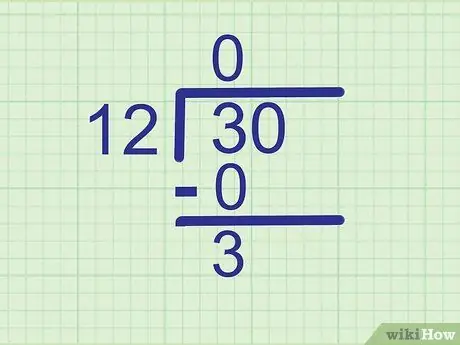
Étape 3. Soustrayez pour trouver le reste
Soustrayez le produit que vous venez de calculer du chiffre situé juste au-dessus. Écrivez la réponse sur une nouvelle ligne, en dessous.
-
Exemple:
3 - 0 = 3, alors écrivez
Étape 3. juste en dessous de 0.
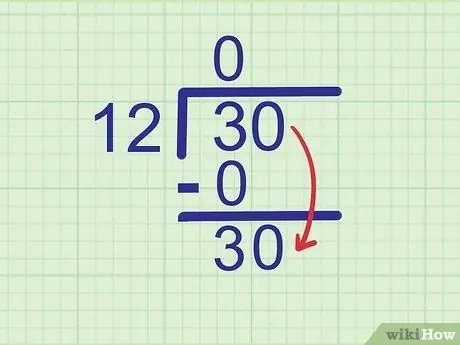
Étape 4. Abaissez le chiffre suivant
Déposez le chiffre suivant du nombre divisé à côté du nombre que vous venez d'écrire.
-
Exemple:
Le nombre qui est divisé est 30. Nous avons vu le nombre 3, donc le prochain chiffre qui doit être abaissé est 0. Diminuez le nombre 0 à côté de 3 pour qu'il devienne
Étape 30..
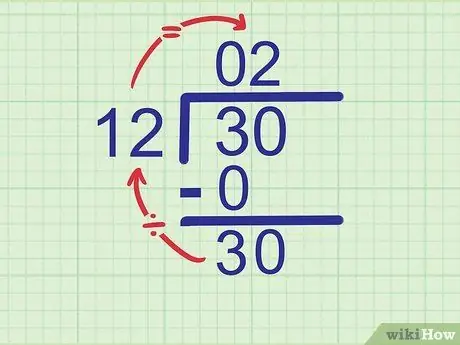
Étape 5. Essayez de diviser le nouveau nombre par le diviseur
Maintenant, répétez la première étape de cette section pour trouver le deuxième chiffre de votre réponse. Cette fois, comparez le diviseur au nombre que vous venez d'écrire sur la rangée du bas.
-
Exemple:
Quel est le quotient de 30 par 12 ? La réponse la plus proche que nous pouvons obtenir est 2 car 12 x 2 = 24. Écrivez
Étape 2. en deuxième place sur la ligne de réponse.
- Si vous n'êtes pas sûr de la réponse, essayez plusieurs multiplications jusqu'à ce que vous trouviez la plus grande réponse qui vous convient. Par exemple, si votre estimation est de 3, calculez 12 x 3 et vous obtenez 36. Ce nombre est trop grand car nous essayons de calculer 30. Essayez de réduire un nombre, 12 x 2 = 24. Ce nombre convient. Donc, 2 est la bonne réponse.

Étape 6. Répétez les étapes ci-dessus pour trouver le numéro suivant
C'est le même processus de division longue que celui utilisé ci-dessus, et pour tout problème de division longue:
- Multipliez le nouveau chiffre de votre réponse par le diviseur: 2 x 12 = 24.
- Écrivez le produit sur une nouvelle ligne, en dessous du nombre qui a été divisé: Écrivez 24 juste en dessous de 30.
- Soustrayez la rangée du bas de la rangée au-dessus: 30 - 24 = 6. Donc, écrivez 6 dans une nouvelle rangée en dessous.

Étape 7. Continuez ce processus jusqu'à ce que vous ayez terminé la dernière ligne de réponses
S'il reste encore des chiffres dans le nombre divisé, réduisez les chiffres et continuez à résoudre le problème de la même manière. Si vous avez terminé la dernière ligne de réponses, passez à l'étape suivante.
-
Exemple:
nous venons d'écrire
Étape 2. dans la dernière ligne de réponse. Passez à l'étape suivante.

Étape 8. Ajoutez des décimales pour « étendre » le nombre divisé si nécessaire
Si le nombre est divisible de manière égale, votre résultat de soustraction final est « 0 ». Cela signifie que vous avez fini de diviser et que vous obtenez une réponse sous la forme d'un nombre entier. Cependant, si vous avez terminé la dernière ligne de réponses et qu'il y a encore des chiffres qui peuvent être divisés, vous devrez « étendre » le nombre divisible en ajoutant un point décimal suivi du nombre 0. Gardez à l'esprit que cela ne ne change pas la valeur du nombre.
-
Exemple:
Nous sommes arrivés à la dernière ligne de réponses, mais la réponse à notre dernière soustraction est "6". Écrivez « 6, 0 » sous le symbole de division longue en ajoutant «, 0 » au dernier chiffre. Écrivez également la virgule décimale au même endroit sur la ligne de réponse, mais n'écrivez rien après cela.

Étape 9. Répétez les mêmes étapes pour trouver le chiffre suivant
La seule différence ici est que vous devez ajouter le point décimal au même endroit sur la ligne de réponse. Une fois que vous avez fait cela, vous pouvez rechercher les chiffres de réponse restants exactement de la même manière.
-
Exemple:
Déposez le nouveau 0 jusqu'à la dernière ligne pour qu'il devienne « 60 ». Puisque 60 divisé par 12 est exactement 5, écrivez
Étape 5. comme dernier chiffre de notre ligne de réponse. N'oubliez pas que nous avons mis une décimale dans notre ligne de réponse. Donc, 2, 5 est la réponse finale à notre question.
Des astuces
- Vous pouvez l'écrire comme un reste (la réponse à 3 1, 2 est donc « 2 restant 6 »). Cependant, comme vous travaillez avec des nombres décimaux, votre professeur peut s'attendre à ce que vous travailliez sur la partie décimale de la réponse.
- Si vous suivez correctement la méthode de division longue, vous aurez toujours une virgule décimale à la bonne position, ou pas de virgule décimale du tout si le nombre est divisible par divisible. N'essayez pas de deviner les décimales. La décimale est souvent différente de la décimale de votre numéro de départ.
- Si le problème de division longue ne dure pas longtemps, vous pouvez vous arrêter et arrondir au nombre le plus proche. Par exemple, pour résoudre 17 4, 2, comptez simplement jusqu'à 4,047… et arrondissez votre réponse à « environ 4,05 ».
-
Rappelez-vous vos termes de division:
- Le nombre à diviser est le nombre à diviser.
- Le diviseur est le nombre utilisé pour diviser.
- Le quotient est la réponse au problème de division mathématique.
- Entier: Divisé par Diviseur = quotient.
Avertissement
N'oubliez pas que 30 12 donnera la même réponse que 3 1, 2. N'essayez pas de « corriger » votre réponse après avoir reculé la virgule
Articles wikiHow connexes
- Conversion de fractions communes en décimales
- Faire une division à long terme
- Diviser les fractions par les fractions
- Division de fractions mixtes






