- Auteur Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- Dernière modifié 2025-06-01 06:06.
Les mathématiques sont difficiles. Il est facile d'oublier même les concepts de base lorsque vous essayez de vous rappeler les nombreux principes et méthodes différents. Voici deux nouvelles façons de simplifier les fractions.
Étape
Méthode 1 sur 4: Utilisation du plus grand facteur commun

Étape 1. Notez les facteurs du numérateur et du dénominateur
Les facteurs sont des nombres que vous pouvez multiplier pour obtenir un autre nombre. Par exemple, 3 et 4 sont des facteurs de 12 car vous pouvez les multiplier ensemble pour obtenir 12. Pour écrire les facteurs d'un nombre, il vous suffit d'écrire tous les nombres qui peuvent être multipliés pour obtenir ce nombre et qui sont divisibles par les facteurs.
-
Notez les facteurs du nombre du plus petit au plus grand, sans oublier d'inclure le facteur 1. Par exemple, voici comment vous écrivez le numérateur et le dénominateur de la fraction 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Étape 2. Trouvez le plus grand facteur commun (GCF) du numérateur et du dénominateur
GCF est le plus grand nombre qui peut diviser également deux nombres ou plus. Après avoir noté tous les facteurs du nombre, il ne vous reste plus qu'à trouver le plus grand nombre qui soit le même dans les deux listes de facteurs.
-
24: 1, 2, 3, 4, 6,
Étape 8., 12, 24.
-
32: 1, 2, 4,
Étape 8., 16, 32.
-
Le GCF de 24 et 32 est de 8 car 8 est le plus grand nombre qui peut diviser également 24 et 32.

Étape 3. Divisez le numérateur et la fraction par le GCF
Maintenant que vous avez le GCF, tout ce que vous avez à faire est de diviser le numérateur et le dénominateur par ce nombre pour simplifier votre fraction dans sa forme la plus simple. Voici comment procéder:
- 24/8 = 3
- 32/8 = 4
- La fraction simple est 3/4.

Étape 4. Vérifiez votre travail
Si vous voulez vous assurer que vous avez correctement simplifié la fraction, il vous suffit de multiplier le nouveau numérateur et le dénominateur par leur GCF pour récupérer la fraction d'origine. Voici comment procéder:
- 3 * 8 = 24
- 4 * 8 = 32
-
Vous êtes revenu à sa forme originale, qui est 24/32.
Vous pouvez également vérifier la fraction pour vous assurer qu'elle ne peut pas être simplifiée davantage. Puisque 3 est un nombre premier, il ne peut être divisé que par 1 et lui-même, et quatre n'est pas divisible par 3, donc la fraction ne peut pas être simplifiée davantage
Méthode 2 sur 4: Continuez à diviser par de petits nombres

Étape 1. Choisissez un petit nombre
En utilisant cette méthode, vous n'avez qu'à choisir un petit nombre, comme 2, 3, 4, 5 ou 7, pour commencer. Regardez les fractions pour vous assurer que chaque partie est divisible par le nombre que vous avez choisi. Par exemple, si vous avez une fraction 24/108, ne choisissez pas 5 car ils ne sont pas divisibles par 5. Cependant, si vous avez une fraction 25/60, 5 est le bon nombre à utiliser.
Pour la fraction 24/32, 2 est un bon nombre. Puisque les deux nombres sont des nombres pairs, ils sont divisibles par 2

Étape 2. Divisez le numérateur et le dénominateur de la fraction par le nombre
La nouvelle fraction consistera en un nouveau numérateur et dénominateur, que vous obtenez après avoir divisé le haut et le bas de la fraction 24/32 par 2. Voici comment procéder:
- 24/2 = 12
- 32/2 = 16
- Votre nouvelle fraction est 12/16.
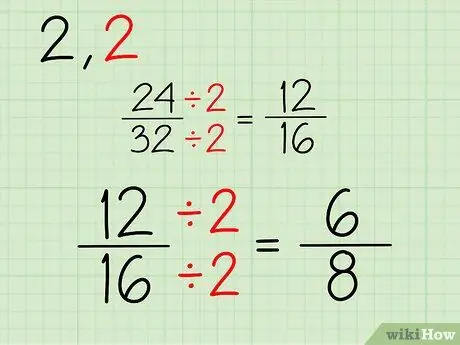
Étape 3. Répétez
Continuez ce processus. Étant donné que les deux nombres sont des nombres pairs, vous pouvez continuer à diviser par 2. Si un ou les deux numérateurs et dénominateurs sont des nombres impairs, vous pouvez essayer de diviser par un autre nombre. Voici le processus pour simplifier la fraction 12/16:
- 12/2 = 6
- 16/2 = 8
- Votre nouvelle fraction est 6/8.

Étape 4. Continuez à diviser le nombre jusqu'à ce qu'il ne soit plus divisible
Le nouveau numérateur et le dénominateur sont également des nombres pairs, vous pouvez donc continuer à diviser par 2. Voici comment procéder:
- 6/2 = 3
- 8/2 = 4
- Votre nouvelle fraction est 3/4.

Étape 5. Assurez-vous que la fraction ne peut pas être simplifiée davantage
Dans la fraction 3/4, 3 est un nombre premier, donc les facteurs ne sont que 1 et lui-même, et 4 n'est pas divisible par 3, donc la fraction ne peut pas être simplifiée davantage. Si le numérateur ou le dénominateur de la fraction ne peut plus être divisé par le nombre que vous avez sélectionné, vous pouvez toujours le diviser par un autre nombre.
Par exemple, si vous avez la fraction 10/40 et que vous divisez le numérateur et le dénominateur par 5, le résultat est 2/8. Vous ne pouvez pas continuer à diviser le numérateur et la fraction par 5, mais vous pouvez diviser les deux par 2 pour que le résultat final soit 1/4

Étape 6. Vérifiez votre travail
Multipliez à nouveau 3/4 par 2/2 trois fois, pour vous assurer d'obtenir la fraction initiale, qui est 24/32. Voici comment procéder:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Notez que vous divisez 24/32 par 2 * 2 * 2, ce qui équivaut à diviser par 8, le plus grand GCF de 24 et 32.
Méthode 3 sur 4: Écrire les facteurs

Étape 1. Écrivez votre fraction
Laissez un grand espace sur le côté droit de votre papier - vous en aurez besoin pour noter les facteurs.

Étape 2. Écrivez les facteurs du numérateur et du dénominateur
Seuls les facteurs des deux. Le moyen le plus simple est d'écrire les facteurs les uns sur les autres. Commencez par le chiffre 1 et notez les facteurs.
-
Par exemple, si votre fraction est 24/60, commencez par 24.
Écrivez: 24 -- 1, 2, 3, 4, 6, 8, 12, 24
-
Ensuite, le nombre 60.
Écrivez: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Étape 3. Trouvez et divisez par le plus grand facteur commun
Ce terme peut être écrit comme GCF dans votre livre imprimé. Quel est le plus grand nombre qui peut diviser le numérateur et le dénominateur ? Quel que soit le nombre, divisez les deux nombres par ce nombre.
Pour notre exemple, le plus grand nombre qui est un facteur des deux nombres est 12. Ainsi, nous divisons 24 par 12 et 60 par 12, ce qui nous donne 2/5 - notre fraction simple
Méthode 4 sur 4: Utilisation d'un arbre à facteurs premiers

Étape 1. Trouvez les facteurs premiers du numérateur et du dénominateur
Un nombre premier est un nombre qui ne peut être divisé par aucun autre nombre (autre que lui-même et 1, bien sûr). 2, 3, 5, 7 et 11 sont des exemples de nombres premiers.
- Commencez par le numérateur. À partir de 24, divisé en 2 et 12. Puisque 2 est déjà un nombre premier, vous n'avez plus besoin de le diviser ! Ensuite, divisez 12 en 2 nombres: 2 et 6. 2 sont des nombres premiers - super ! Divisez maintenant 6 en 2 nombres: 2 et 3. Vous avez maintenant 2, 2, 2 et 3 comme nombres premiers.
- Travaillez maintenant sur le dénominateur. À partir de 60, divise ton arbre en 2 et 30. 30 puis divise en 2 et 15. Ensuite, divise 15 en 3 et 5, qui sont tous deux des nombres premiers. Vous avez maintenant 2, 2, 3 et 5 comme nombres premiers.
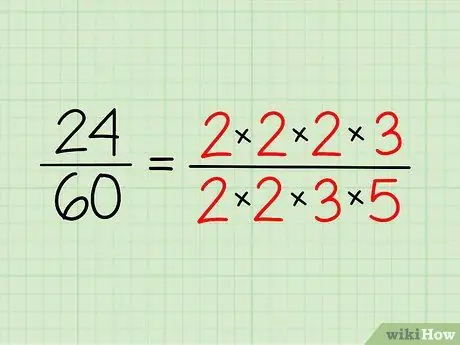
Étape 2. Écrivez la factorisation première de chaque nombre
Notez les nombres premiers que vous avez pour chaque nombre et écrivez-les sous forme de multiplication. Vous n'avez pas besoin de le multiplier - c'est juste un moyen de le rendre plus facile à voir.
- Donc, pour 24, vous avez 2 x 2 x 2 x 3 = 24.
- Pour 60, vous avez 2 x 2 x 3 x 5 = 60

Étape 3. Éliminez les mêmes facteurs
Tout numéro faisant partie des deux numéros peut être supprimé. Dans cet exemple, les facteurs égaux sont une paire de 2 et un 3. Au revoir !
- Les autres sont 2 et 5 - ou 2/5 ! La même réponse que nous avons obtenue ci-dessus.
- Si le numérateur et le dénominateur de la fraction sont des nombres pairs, ne divisez pas simplement par deux. Continuez à faire la division jusqu'à ce que le nombre que vous obtenez ne puisse plus être divisé.






