- Auteur Jason Gerald [email protected].
- Public 2024-01-15 08:14.
- Dernière modifié 2025-06-01 06:06.
La valeur P est une mesure statistique qui aide les scientifiques à déterminer si leur hypothèse est correcte. La valeur P est utilisée pour déterminer si les résultats de leur expérience se situent dans la plage de valeurs normales pour les choses étudiées. Habituellement, si la valeur P d'un ensemble de données tombe en dessous d'une certaine valeur prédéterminée (par exemple, 0,05), les scientifiques rejetteront l'hypothèse nulle de leur expérience - en d'autres termes, ils écarteront une hypothèse où la variable expérimentale a pas d'effet significatif sur le résultat. Aujourd'hui, les valeurs p se trouvent généralement dans les tableaux de référence en calculant la valeur du chi carré.
Étape

Étape 1. Déterminez les résultats attendus de votre expérience
Habituellement, lorsque les scientifiques mènent une expérience et examinent les résultats, ils ont déjà une idée des résultats normaux ou ordinaires à l'avance. Cela peut être basé sur les résultats d'expériences précédentes, des ensembles de données d'observation fiables, de la littérature scientifique et/ou d'autres sources. Pour votre expérience, déterminez votre résultat attendu et notez-le sous forme de nombre.
Exemple: supposons qu'une étude précédente ait montré qu'au niveau national, les contraventions pour excès de vitesse étaient délivrées plus souvent aux voitures rouges qu'aux voitures bleues. Supposons que le résultat moyen au niveau national montre un ratio de 2:1 avec un ratio de voitures rouges supérieur. Nous voulons savoir si la police de notre ville a également la même tendance en analysant les contraventions pour excès de vitesse émises par la police de notre ville. Si nous prenions un échantillon aléatoire de 150 contraventions pour excès de vitesse données à la fois aux voitures rouges et bleues de notre ville, nous nous attendrions à 100 pour voiture rouge et 50 pour les voitures bleues si l'unité de police de notre ville donne une contravention selon la comparaison au niveau national.

Étape 2. Déterminez vos observations expérimentales
Maintenant que vous avez déterminé votre valeur attendue, vous pouvez exécuter votre expérience et trouver la vraie valeur (ou observation). Encore une fois, notez le résultat sous forme de nombre. Si nous manipulons certaines conditions expérimentales et que les résultats observés diffèrent des résultats attendus, deux possibilités existent: soit cela s'est produit par hasard, soit c'est notre manipulation des variables expérimentales qui a causé cette différence. Le but de trouver la valeur p est essentiellement de déterminer si les résultats observés diffèrent des résultats attendus à un point où l'hypothèse nulle - l'hypothèse qu'il n'y a pas de relation entre la variable expérimentale et les résultats observés - ne peut pas être rejetée.
Exemple: supposons que, dans notre ville, nous sélectionnions au hasard 150 contraventions pour excès de vitesse qui sont attribuées à la fois aux voitures rouges et bleues. On a 90 un ticket pour une voiture rouge et 60 pour la voiture bleue. Ceci est différent du résultat que nous attendions, c'est-à-dire 100 et 50. Notre manipulation expérimentale (dans ce cas, changer la source de données de nationale à locale) a-t-elle modifié les résultats, ou notre police municipale avait-elle les mêmes tendances que le niveau national, et nous avons juste observé une coïncidence ? La valeur p nous aidera à le déterminer.

Étape 3. Déterminez les degrés de liberté de votre expérience
Les degrés de liberté sont une mesure de la quantité de variabilité dans l'étude, qui est déterminée par le nombre de catégories que vous examinez. L'équation des degrés de liberté est Degrés de liberté = n-1, où n est le nombre de catégories ou de variables analysées dans votre expérience.
-
Exemple: Notre expérience comporte deux catégories de résultats: une pour la voiture rouge et une pour la voiture bleue. Ainsi, dans notre expérience, nous avons 2-1 = 1 degré de liberté.
Si nous comparons les voitures rouges, bleues et vertes, nous aurons
Étape 2. degrés de liberté et ainsi de suite.

Étape 4. Comparez les résultats attendus avec les résultats observés en utilisant le chi carré
Chi carré (écrit x2) est une valeur numérique qui mesure la différence entre les valeurs attendues et observées de l'expérience. L'équation du chi carré est: X2 = ((o-e)2/e), où o est la valeur observée et e est la valeur attendue. Additionnez les résultats de cette équation pour tous les résultats possibles (voir ci-dessous).
- Notez que cette équation utilise l'opérateur (sigma). En d'autres termes, vous devez calculer ((|o-e|-.05)2/e) pour chaque résultat possible, puis additionnez les résultats pour obtenir la valeur du chi carré. Dans notre exemple, nous avons deux résultats: une voiture qui obtient un ticket rouge ou un ticket bleu. Ainsi, nous pouvons calculer ((o-e)2/e) deux fois - une fois pour la voiture rouge et une fois pour la voiture bleue.
-
Exemple: insérons nos valeurs attendues et nos observations dans l'équation x2 = ((o-e)2/e). Rappelez-vous qu'à cause de l'opérateur sigma, nous devons calculer ((o-e)2/e) deux fois - une fois pour la voiture rouge et une fois pour la voiture bleue. Les étapes de traitement sont les suivantes:
- X2 = ((90-100)2/100) + (60-50)2/50)
- X2 = ((-10)2/100) + (10)2/50)
- X2 = (100/100) + (100/50) = 1 + 2 = 3.

Étape 5. Choisissez un niveau d'importance
Maintenant que nous connaissons les degrés de liberté de notre kit expérimental et la valeur du chi carré, il n'y a qu'une dernière chose à faire avant de pouvoir trouver notre valeur p: nous devons déterminer le niveau de signification. Fondamentalement, le niveau de signification est une mesure de notre degré de certitude quant à nos résultats - un faible niveau de signification correspond à une faible probabilité que le résultat d'une expérience soit dû au hasard et vice versa. Le niveau de signification est écrit sous forme décimale (par exemple 0,01), qui correspond au pourcentage de probabilité que le résultat de l'expérience soit dû au hasard (dans ce cas, 1 %).
- Par convention, les scientifiques fixent généralement une valeur de signification pour leurs expériences à 0,05 ou 5 %. Cela signifie que les résultats expérimentaux qui correspondent à ce niveau de significativité ont, au maximum, 5% de chance de coïncidence. En d'autres termes, il y a 95% de chances que les résultats soient dus à la manipulation par le scientifique des variables expérimentales, et non au hasard. Pour la plupart des expériences, une confiance de 95 % sur la relation entre les deux variables est considérée comme ayant réussi à démontrer la relation entre les deux.
- Exemple: Pour notre exemple de voiture rouge et bleue, suivons l'accord scientifique et déterminons notre niveau de signification de 0, 05.
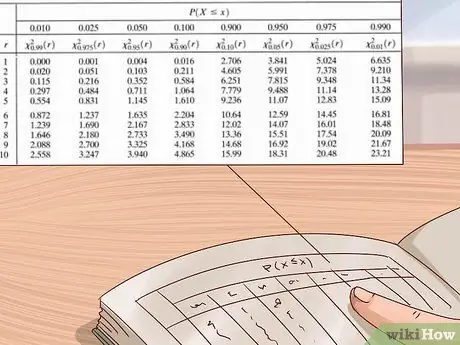
Étape 6. Utilisez le tableau de distribution du chi carré pour estimer votre valeur p
Les scientifiques et les statisticiens utilisent de grands tableaux de valeurs pour calculer les valeurs p pour leurs expériences. Ce tableau est généralement écrit avec l'axe vertical à gauche indiquant les degrés de liberté et l'axe horizontal en haut indiquant les valeurs p. Utilisez ce tableau en trouvant d'abord vos degrés de liberté, puis en lisant les lignes de gauche à droite jusqu'à ce que vous trouviez la première valeur supérieure à votre valeur du chi carré. Regardez la valeur p en haut de la colonne - votre valeur p se situe entre cette valeur et la prochaine valeur la plus grande (la valeur de droite est à sa gauche).
- Les tableaux de distribution du chi carré sont disponibles à partir de diverses sources - ils peuvent facilement être trouvés en ligne ou dans des manuels de sciences ou de statistiques. Si vous n'en avez pas, utilisez le tableau montré sur la photo ci-dessus ou un tableau en ligne gratuit, comme celui fourni par medcalc.org ici.
-
Exemple: Notre chi carré est 3. Utilisons donc le tableau de distribution du chi carré de la photo ci-dessus pour trouver une valeur p approximative. Puisque nous savons que notre expérience n'a
Étape 1. degrés de liberté, nous commencerons par la table du haut. Nous allons de gauche à droite dans cette rangée jusqu'à ce que nous trouvions une valeur supérieure à
Étape 3. - notre valeur chi carré. La première valeur que nous trouvons est 3,84. En regardant cette colonne, nous voyons que la valeur p correspondante est de 0,05. Cela signifie que notre valeur p est entre 0,05 et 0,1 (valeur de p la plus grande suivante dans le tableau).

Étape 7. Décidez de rejeter ou de défendre votre hypothèse nulle
Puisque vous avez trouvé une valeur p approximative pour votre expérience, vous pouvez décider de rejeter ou non l'hypothèse nulle de votre expérience (pour rappel, il s'agit de l'hypothèse selon laquelle la variable expérimentale que vous avez manipulée n'a eu aucun effet sur les résultats que vous avez observés). Si votre valeur p est inférieure à votre valeur de signification, félicitations - vous avez prouvé qu'il existe une forte probabilité qu'il existe une relation entre les variables que vous avez manipulées et vos observations. Si votre valeur p est supérieure à votre valeur de signification, vous ne pouvez pas dire avec certitude que les résultats que vous observez sont le résultat d'une simple coïncidence ou d'une manipulation de votre expérience.
- Exemple: Notre valeur p est comprise entre 0,05 et 0,1, c'est-à-dire qu'elle n'est en aucun cas inférieure à 0,05, donc, malheureusement, nous ne peut pas rejeter notre hypothèse nulle. Cela signifie que nous n'atteignons pas la limite de confiance minimale de 95 % que nous avons fixée pour qu'on puisse dire que la police de notre ville donne des contraventions aux voitures rouges et bleues dans un rapport assez différent de la moyenne nationale.
- En d'autres termes, il y a 5 à 10 % de chance que nos observations ne soient pas le résultat d'un changement de lieu (analyse de notre ville, et non de l'ensemble), mais soient des coïncidences. Puisque nous recherchons une probabilité inférieure à 5%, nous ne pouvons pas dire que nous convaincu que la police de notre ville a tendance à verbaliser les voitures rouges - il existe une possibilité faible mais statistiquement très différente qu'elle n'ait pas cette tendance.
Des astuces
- Une calculatrice scientifique rendra les calculs beaucoup plus faciles. Vous pouvez également rechercher des calculatrices en ligne.
- Vous pouvez calculer les valeurs p à l'aide de plusieurs programmes informatiques, notamment un tableur couramment utilisé et un logiciel statistique plus spécialisé.






