- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:11.
- Dernière modifié 2025-01-23 12:18.
L'addition de fractions est une connaissance très utile. Cette compétence est très facile à apprendre et à utiliser lorsque vous travaillez sur des problèmes de mathématiques du primaire au secondaire. Cet article explique comment ajouter des fractions afin que vous puissiez le faire en quelques minutes.
Étape
Méthode 1 sur 2: Ajouter des fractions avec le même dénominateur

Étape 1. Vérifiez le dénominateur (le nombre sous le quotient) de chaque fraction
Si les nombres sont les mêmes, alors vous additionnez des fractions avec le même dénominateur. Si les dénominateurs sont différents, lisez la deuxième méthode.
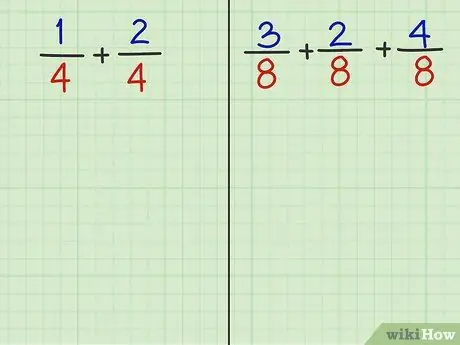
Étape 2. Répondez aux 2 questions suivantes
En lisant la dernière étape de cette méthode, vous devriez pouvoir additionner les fractions des deux questions suivantes.
- Problème 1: 1/4 + 2/4
- Problème 2: 3/8 + 2/8 + 4/8
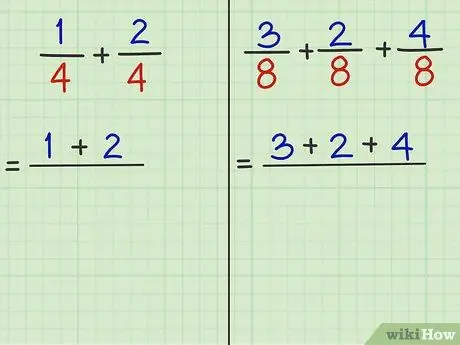
Étape 3. Recueillez les numérateurs (les nombres au-dessus de la division) et additionnez-les
Le numérateur est le nombre au-dessus du quotient. Peu importe le nombre de fractions que vous souhaitez ajouter, vous pouvez ajouter les numérateurs immédiatement si les dénominateurs sont les mêmes.
- Problème 1: 1/4 + 2/4 est la fraction à ajouter. "1" et "2" sont des numérateurs. Donc, 1 + 2 = 3.
- Problème 2: 3/8 + 2/8 + 4/8 est la fraction à ajouter. "3" et "2" et "4" sont des numérateurs. Donc, 3 + 2 + 4 = 9.

Étape 4. Déterminez la nouvelle fraction à partir de la somme
Notez le numérateur obtenu à l'étape 2. Ce nombre est nouveau numérateur. Écris le dénominateur, qui est le même nombre sous la bissectrice de chaque fraction. Vous n'avez pas besoin de faire les calculs si les dénominateurs sont les mêmes. Ce numéro est nouveau dénominateur et est toujours égal à l'ancien dénominateur lorsque vous additionnez des fractions avec le même dénominateur.
- Problème 1: 3 est le nouveau numérateur et 4 est le nouveau dénominateur. Ainsi, la réponse à la question 1 est 3/4. 1/4 + 2/4 = 3/4.
- Problème 2: 9 est le nouveau numérateur et 8 est le nouveau dénominateur. Ainsi, la réponse à la question 2 est 9/8. 3/8 + 2/8 + 4/8 = 9/8.
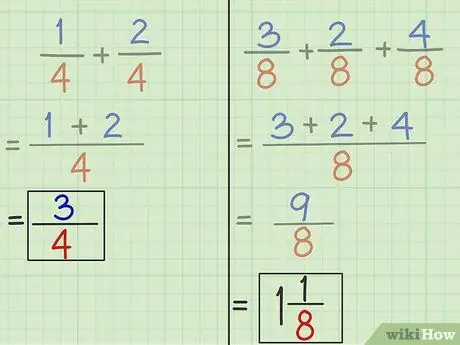
Étape 5. Simplifiez les fractions si nécessaire
N'oubliez pas de simplifier la nouvelle fraction pour rendre l'écriture plus simple.
-
Si le numérateur plus gros au lieu d'un dénominateur comme le résultat de l'addition du problème 2, cela signifie que nous obtenons 1 mois entier après avoir simplifié la fraction. Divisez le numérateur par le dénominateur ou 9 divisé par 8. Le résultat est un entier 1 restant 1. Écrivez entiers devant la fraction et le reste devient le numérateur d'une nouvelle fraction de même dénominateur.
9/8 = 1 1/8.
Méthode 2 sur 2: Ajout de fractions avec différents dénominateurs

Étape 1. Vérifiez le dénominateur (le nombre sous le quotient) de chaque fraction
Si les dénominateurs sont différents, vous êtes additionner des fractions avec des dénominateurs différents. Lisez les étapes suivantes car vous devez rendre les dénominateurs égaux avant d'ajouter des fractions.
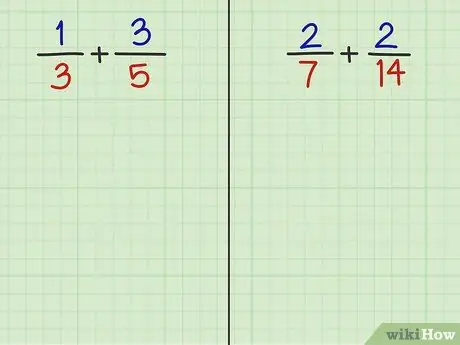
Étape 2. Résolvez les 2 questions suivantes
En lisant la dernière étape de cette méthode, vous devriez pouvoir additionner les fractions des deux questions suivantes.
- Problème 3: 1/3 + 3/5
- Question 4: 2/7 + 2/14

Étape 3. Faites correspondre les dénominateurs
Pour ce faire, multipliez les dénominateurs des deux fractions ci-dessus. Un moyen facile d'égaliser les dénominateurs est de multiplier les dénominateurs des deux fractions. Si l'un des dénominateurs est un multiple de l'autre, trouvez le plus petit commun multiple des deux dénominateurs.
-
Problème 3:
3 x 5 = 15. Ainsi, le nouveau dénominateur des deux fractions est 15.
-
Problème 4:
14 est un multiple de 7. Par conséquent, il suffit de multiplier 7 par 2 pour obtenir 14. Ainsi, le nouveau dénominateur des deux fractions est 14.

Étape 4. Multipliez le numérateur et le dénominateur de la première fraction par le dénominateur de la deuxième fraction
Cette étape ne change pas la valeur de la fraction, mais la fraction semble changer pour correspondre au dénominateur. La valeur fractionnaire reste la même.
-
Problème 3:
1/3 x 5/5 = 5/15.
-
Problème 4:
Pour ce problème, il suffit de multiplier la première fraction par 2/2 pour que les dénominateurs soient égaux.
2/7 x 2/2 = 4/14

Étape 5. Multipliez le numérateur et le dénominateur de la deuxième fraction par le dénominateur de la première fraction
Semblable aux étapes ci-dessus, nous ne modifions pas la valeur de la fraction, mais la fraction semble changer pour égaliser le dénominateur. La valeur fractionnaire reste la même.
-
Problème 3:
3/5 x 3/3 = 9/15.
-
Problème 4:
Nous n'avons pas besoin de multiplier la deuxième fraction car les dénominateurs sont les mêmes.

Étape 6. Écrivez les deux nouvelles fractions dans l'ordre
À ce stade, nous n'avons pas additionné les deux fractions, bien que nous le puissions. Dans l'étape ci-dessus, nous avons multiplié chaque fraction par 1. Maintenant, nous voulons nous assurer que les fractions que nous voulons additionner ont le même dénominateur.
-
Problème 3:
au lieu de 1/3 + 3/5, la fraction devient 5/15 + 9/15
-
Problème 4:
Au lieu de 2/7 + 2/14, la fraction devient 4/14 + 2/14

Étape 7. Additionnez les numérateurs des deux fractions ensemble
Le numérateur est le nombre au-dessus du quotient.
-
Problème 3:
5 + 9 = 14. 14 est le nouveau numérateur.
-
Problème 4:
4 + 2 = 6. 6 est le nouveau numérateur.

Étape 8. Écrivez le dénominateur commun (à l'étape 2) sous le nouveau numérateur ou utilisez le dénominateur de la fraction multipliée par 1 pour égaliser le dénominateur
-
Problème 3:
15 est le nouveau dénominateur.
-
Problème 4:
14 est le nouveau dénominateur.

Étape 9. Écrivez un nouveau numérateur et un nouveau dénominateur
-
Problème 3:
14/15 est la réponse 1/3 + 3/5 = ?
-
Problème 4:
6/14 est la réponse 2/7 + 2/14 = ?

Étape 10. Simplifiez et réduisez les fractions
Pour simplifier les fractions, divisez le numérateur et le dénominateur par le plus grand facteur commun des deux nombres.
-
Problème 3:
14/15 ne peut pas être simplifié.
-
Problème 4:
6/14 peut être réduit à 3/7 après avoir divisé le numérateur et le dénominateur par 2 comme le plus grand facteur commun de 6 et 14.
Des astuces
- Avant d'ajouter des fractions, assurez-vous que les dénominateurs sont les mêmes.
- N'additionnez pas les dénominateurs. Si les dénominateurs sont les mêmes, utilisez le nombre comme dénominateur après avoir additionné les fractions.
- Si vous souhaitez ajouter des fractions avec des nombres composés de nombres entiers et de fractions, convertissez ces nombres en fractions et additionnez-les selon les instructions ci-dessus.






