- Auteur Jason Gerald [email protected].
- Public 2024-01-15 08:14.
- Dernière modifié 2025-01-23 12:18.
La moyenne géométrique est une autre façon de trouver la valeur moyenne d'un ensemble de nombres, ce qui se fait en multipliant les valeurs avant de prendre les racines, au lieu d'additionner les valeurs et de les diviser comme dans une moyenne arithmétique. La moyenne géométrique peut être utilisée pour calculer le taux de rendement moyen dans l'analyse financière ou pour montrer le taux de croissance de quelque chose sur une période de temps. Pour trouver la moyenne géométrique, multipliez toutes les valeurs avant l'enracinement par, qui est le nombre total de nombres dans l'ensemble. Vous pouvez également utiliser la fonction logarithme de votre calculatrice pour trouver la moyenne géométrique, si vous préférez.
Étape
Méthode 1 sur 2: Recherche de la moyenne géométrique d'un ensemble de valeurs
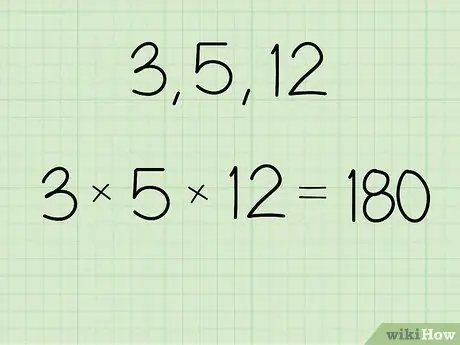
Étape 1. Multipliez la valeur pour laquelle vous souhaitez trouver la moyenne géométrique
Vous pouvez utiliser une calculatrice ou calculer manuellement pour obtenir le résultat. Notez les résultats pour ne pas les oublier.
- Par exemple, si l'ensemble de nombres est 3, 5 et 12, calculez: (3 x 5 x 12) = 180.
- Pour un autre exemple, si vous voulez trouver la moyenne géométrique de l'ensemble des nombres 2 et 18, écrivez: (2 x 18) = 36.
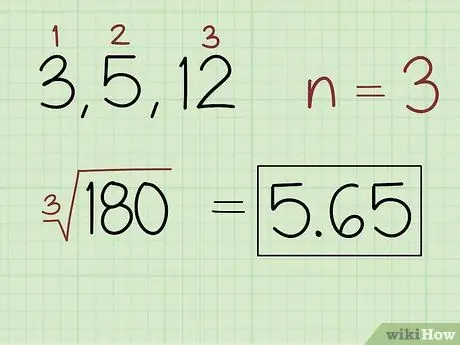
Étape 2. Trouvez la racine nième du produit, où n est le nombre de valeurs dans l'ensemble
Comptez le nombre de nombres dans l'ensemble pour obtenir la valeur. Utilisez les valeurs pour spécifier la racine qui doit être utilisée dans le produit. Par exemple, utilisez la racine carrée si l'ensemble contient 2 nombres, la racine cubique si l'ensemble contient 3 nombres, et ainsi de suite. Utilisez une calculatrice pour résoudre l'équation et écrivez la réponse.
- Par exemple, pour un ensemble de nombres 3, 5 et 12, écrivez: (180) 5, 65.
- Dans le deuxième exemple avec l'ensemble contenant 2 et 18, écrivez: (36) = 6.
Variation:
Vous pouvez également écrire la racine comme exposant de 1/, s'il est plus facile d'écrire sur une calculatrice. Par exemple, pour l'ensemble des nombres 3, 5 et 12, écrivez (180)1/3 au lieu de (180).
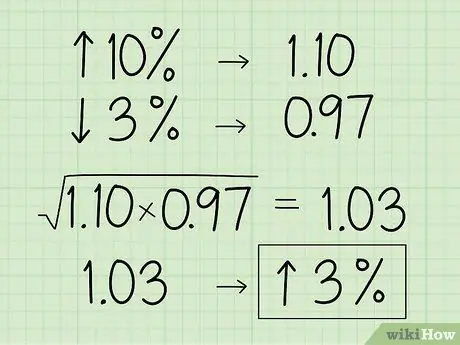
Étape 3. Convertissez le pourcentage en son équivalent multiplicateur décimal
Si l'ensemble de nombres est écrit sous forme d'augmentation ou de diminution en pourcentage, essayez de ne pas utiliser la valeur en pourcentage dans la moyenne géométrique car les résultats ne seront pas précis. Si le pourcentage augmente, déplacez la virgule décimale de deux chiffres vers la gauche et ajoutez 1. Si le pourcentage diminue, déplacez la virgule décimale de 2 chiffres vers la gauche et soustrayez de 1.
- Par exemple, supposons que vous souhaitiez trouver la moyenne géométrique des valeurs d'objets qui augmente de 10 %, puis diminue de 3 %.
- Convertissez 10 % en nombre décimal et ajoutez 1 pour obtenir 1, 10.
- Ensuite, convertissez 3 % en nombre décimal et soustrayez 1 pour obtenir 0,97.
- Utilisez les deux décimales pour trouver la moyenne géométrique: (1, 10 x 0,97) 1,03.
- Convertissez le nombre en pourcentage en décalant la virgule décimale de 2 chiffres vers la droite et en soustrayant 1 pour obtenir une augmentation de 3 % de la valeur.
Méthode 2 sur 2: Calcul de la moyenne géométrique à l'aide de logarithmes

Étape 1. Additionnez les valeurs logarithmiques pour chaque nombre de l'ensemble
La fonction LOG de la calculatrice prend la base 10 d'un nombre et détermine combien vous devez multiplier par 10 pour qu'il soit égal au nombre. Recherchez la fonction LOG sur la calculatrice, qui se trouve généralement sur le côté gauche du bouton. Cliquez sur le bouton LOG et entrez le premier numéro de l'ensemble. Tapez « + » avant d'entrer LOG pour le deuxième nombre. Continuez à séparer la fonction LOG pour chaque nombre par un signe plus avant d'obtenir la somme.
- Par exemple, pour les ensembles 7, 9 et 12, tapez log(7) + log(9) + log(12), puis appuyez sur "=" sur la calculatrice. Si la fonction a été calculée, le nombre sera d'environ 2,878521796.
- Vous pouvez également calculer chaque logarithme séparément avant de les additionner tous ensemble.
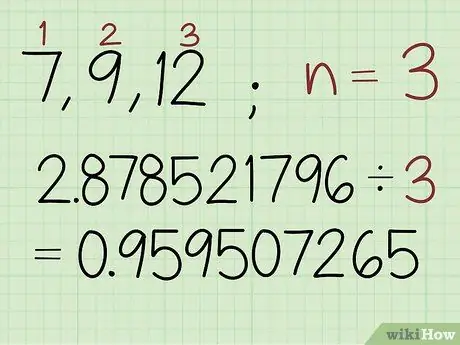
Étape 2. Divisez la somme des valeurs logarithmiques par le nombre de nombres de l'ensemble
Comptez le nombre de valeurs dans l'ensemble et divisez le nombre obtenu précédemment par ce nombre. Le résultat est le logarithme de la moyenne géométrique.
Dans cet exemple, il y a 3 nombres dans l'ensemble alors tapez: 2, 878521796 / 3 0, 959507265

Étape 3. Trouvez l'antilog du quotient pour déterminer la moyenne géométrique
La fonction antilog est l'inverse de la fonction LOG sur la calculatrice et reconvertit la valeur en base 10. Recherchez le symbole « 10X sur la calculatrice, qui est généralement une fonction secondaire du bouton LOG. Appuyez sur le bouton « 2nd » dans le coin supérieur gauche de la calculatrice suivi du bouton LOG pour activer l'antilog. Tapez le quotient trouvé dans la dernière étape avant de résoudre l'équation.
Pour cet exemple, la calculatrice affichera: 10(0, 959507265) ≈ 9, 11.
Des astuces
- Vous ne pouvez pas trouver la moyenne géométrique des nombres négatifs.
- Tous les ensembles qui ont 0 auront une moyenne géométrique de 0.






