- Auteur Jason Gerald [email protected].
- Public 2024-02-01 14:13.
- Dernière modifié 2025-01-23 12:18.
Tout ce dont vous avez besoin pour calculer la vitesse moyenne est la cylindrée totale. ou changement de position, et temps total. N'oubliez pas que la vitesse calcule également la direction et la vitesse d'un objet, alors incluez une direction dans votre réponse, telle que « nord », « avant » ou « gauche ». Si votre problème de calcul de vitesse implique également une accélération constante, vous pouvez apprendre un moyen rapide de trouver la réponse encore plus facilement.
Étape
Méthode 1 sur 2: Calcul de la vitesse moyenne de déplacement et du temps

Étape 1. N'oubliez pas que la vitesse comprend à la fois la vitesse et la direction d'un objet
La vitesse décrit la vitesse à laquelle la position d'un objet change. Cela a à voir non seulement avec la vitesse à laquelle l'objet se déplace, mais aussi avec sa direction. "100 mètres par seconde vers le sud" est une valeur de vitesse différente de "100 mètres par seconde vers l'est".
- Les quantités qui ont une direction sont appelées quantités vectorielles. Cette quantité peut être distinguée d'une quantité sans direction appelée quantité scalaire en écrivant une flèche au-dessus de la variable. Par exemple, la notation v représente le taux, tandis que la notation v → représente la vitesse ou la vitesse + direction. La notation v utilisée dans cet article représente la vitesse.
- Dans les problèmes scientifiques, vous devez utiliser des mètres ou d'autres unités métriques pour exprimer la distance, tandis que pour des besoins quotidiens, vous pouvez utiliser n'importe quelle unité de votre choix.
Étape 2. Trouvez la valeur de déplacement total
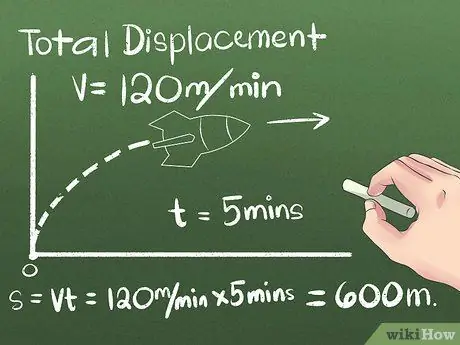
Le déplacement est le changement de position d'un objet, ou la distance et la direction entre ses points de départ et d'arrivée. La direction dans laquelle l'objet se déplace avant d'atteindre sa position finale peut être négligée, car seule la distance entre les points de départ et d'arrivée est prise en compte. Pour le premier exemple, nous utiliserons un objet se déplaçant à vitesse constante dans une direction:
- Supposons qu'une fusée se déplace vers le nord pendant 5 minutes à une vitesse constante de 120 mètres par minute. Pour calculer la position finale, utilisez la formule s = vt, ou utilisez la réflexion pratique pour calculer la distance parcourue par la fusée après cela (5 minutes) (120 mètres/minute) = 600 mètres au nord du point de départ.
- Pour les problèmes impliquant une accélération constante, vous pouvez les résoudre avec s = vt + à2, ou utilisez la méthode courte décrite dans une autre section pour trouver la réponse.
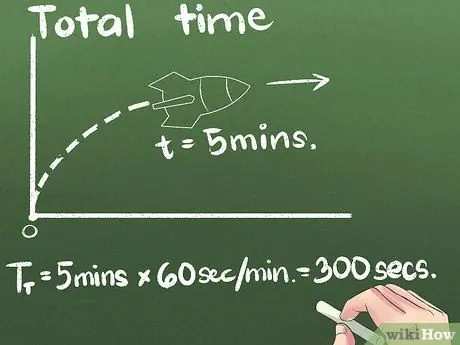
Étape 3. Trouvez le temps total passé
Dans notre exemple, la fusée avance pendant 5 minutes. Vous pouvez exprimer la vitesse moyenne dans n'importe quelle unité de temps, mais la seconde est l'unité standard scientifique internationale. Nous allons changer les unités de secondes dans cet exemple: (5 minutes) x (60 secondes/minute) = 300 secondes.
Même dans les problèmes scientifiques, si la question utilise l'heure ou une unité de temps plus grande, il sera plus facile de calculer d'abord la vitesse, puis de convertir la réponse finale en mètres/seconde
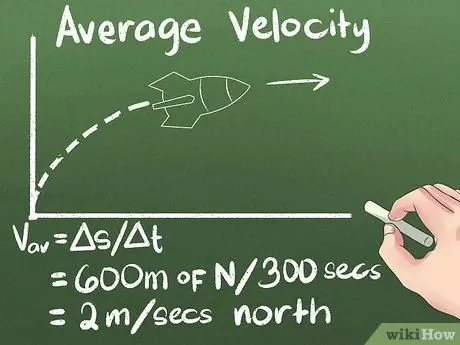
Étape 4. Calculez la vitesse moyenne en tant que déplacement dans le temps
Si vous savez à quelle distance un objet se déplace et combien de temps il faudra pour y arriver, vous saurez à quelle vitesse il se déplace. Donc, pour l'exemple que nous utilisons, la vitesse moyenne de la fusée est (600 mètres au nord) / (300 secondes) = 2 mètres/seconde nord.
- N'oubliez pas d'inclure une direction (comme « avant » ou « nord »).
- Dans la formule vun V = s/Δt. Le symbole delta signifie "changement", donc s/Δt signifie "changement de position sur une période de temps".
- La vitesse moyenne peut être écrite comme vun V, ou comme un v avec une ligne horizontale au-dessus.

Étape 5. Résolvez des problèmes plus complexes
Si un objet change de direction ou de vitesse, ne vous y trompez pas. La vitesse moyenne est toujours "seulement" calculée à partir du déplacement total et du temps total. Ce qui se passe entre les points de début et de fin, vous pouvez l'ignorer. Voici quelques exemples d'un objet se déplaçant avec le même déplacement et le même temps total, et donc, la même vitesse moyenne:
- Anna marche vers l'ouest à 1 mètre/s pendant 2 secondes, puis accélère soudainement à 3 mètres/seconde et continue à marcher vers l'ouest pendant 2 secondes. Le déplacement total est de (1 m/s vers l'ouest)(2 sec) + (3 m/s vers l'ouest)(2 sec) = 8 mètres vers l'ouest. Le temps total est de 2 secondes + 2 secondes = 4 secondes. La vitesse moyenne est donc de 8 mètres à l'ouest / 4 secondes = 2 mètres/seconde ouest.
-
Bart marche vers l'ouest à 5 mètres/sec pendant 3 secondes, puis se retourne et marche vers l'est à 7 mètres/sec pendant 1 seconde. Nous pouvons considérer le mouvement vers l'est comme un "mouvement négatif vers l'ouest", donc le déplacement total est = (5 mètres/sec vers l'ouest) (3 sec) + (-7 m/s vers l'ouest) (1 sec) = 8 mètres. Temps total = 4 secondes. Vitesse moyenne = 8 mètres à l'ouest / 4 secondes = 2 mètres/seconde ouest.
-
Charlotte a marché 1 mètre vers le nord, puis 8 mètres vers l'ouest, puis 1 mètre vers le sud. Le temps qu'il faut pour effectuer l'ensemble du trajet est de 4 secondes. Dessinez le diagramme sur une feuille de papier et vous verrez que le point final est à 8 mètres à l'ouest du point de départ, donc cette valeur est le déplacement. Le temps total que cela prend est de 4 secondes, donc la vitesse moyenne est de 8 mètres à l'ouest / 4 secondes = 2 mètres/seconde ouest.
Méthode 2 sur 2: Calcul de la vitesse moyenne d'accélération fixe

Calculer la vitesse moyenne Étape 6 Étape 1. Considérez la vitesse initiale et l'accélération constante
Disons que notre problème est "Un vélo se déplace vers la droite avec une vitesse de 5 m/s, avec une accélération constante de 2 m/s2. Si ce vélo bouge pendant 5 secondes, quelle est sa vitesse moyenne ?"
Si l'unité "mètre/seconde2" pour vous embrouiller, écrivez-le sous la forme "mètres/seconde/seconde" ou "mètres par seconde par seconde." Une accélération de 2 mètres/seconde/seconde signifie que la vitesse augmente de 2 mètres par seconde chaque seconde.

Calculer la vitesse moyenne Étape 7 Étape 2. Utilisez l'accélération pour trouver la vitesse finale
L'accélération, désignée par la notation a, est le taux de changement de vitesse (ou taux). La vitesse augmente à un taux d'augmentation constant. Vous pouvez dessiner un tableau en utilisant l'accélération pour trouver la vitesse à différents moments tout au long du trajet à vélo. Nous devons créer ce tableau pour trouver le point final du problème (à t = 5 secondes), mais nous allons créer un tableau plus long pour vous faciliter la compréhension de ce concept:
- Au point de départ (temps t = 0 seconde), le vélo se déplace à une vitesse de 5 mètres/s.
- Après 1 seconde (t = 1), le vélo se déplace à une vitesse de 5 mètres/seconde + à = 5 mètres/seconde + (2 mètres/seconde2)(1 seconde) = 7 mètres/seconde.
- A t = 2, le vélo se déplace vers la droite à une vitesse de 5+(2)(2) = 9 mètres/sec.
- A t = 3, le vélo se déplace vers la droite à une vitesse de 5+(2)(3) = 11 mètres/sec.
- A t = 4, le vélo se déplace vers la droite à une vitesse de 5+(2)(4) = 13 mètres/sec.
- A t = 5, le vélo se déplace vers la droite avec une vitesse de 5+(2)(5) = 15 mètres/seconde.

Calculer la vitesse moyenne Étape 8 Étape 3. Utilisez cette formule pour trouver la vitesse moyenne
Si et "seulement" si l'accélération est constante, la vitesse moyenne sera égale à la valeur moyenne de la somme des vitesses finale et initiale. (vF +vje)/2. Pour notre exemple de problème ci-dessus, la vitesse initiale du vélo est vje 5 mètres/seconde. Après calcul, la vitesse finale est vF 15 mètres/seconde. En additionnant ces deux valeurs, on obtient (15 mètres/seconde + 5 mètres/seconde) / 2 = (20 mètres/seconde) / 2 = 10 mètres/seconde direction droite.
- N'oubliez pas d'inclure la direction, dans ce cas « droit ».
- Ce terme peut s'écrire v0 (vitesse au temps 0, ou vitesse initiale) et v (vitesse finale).

Calculer la vitesse moyenne Étape 9 Étape 4. Comprenez intuitivement la formule de la vitesse moyenne
Pour trouver la vitesse moyenne, nous pouvons utiliser la vitesse à n'importe quel point et trouver la moyenne pour chacun d'eux. (C'est la définition d'une moyenne.) Puisque cela nécessite un calcul ou un temps infini, comprenez cette formule de manière plus intuitive. Au lieu de prendre à chaque fois, calculez la vitesse moyenne des deux points temporels et voyez les résultats. Un point dans le temps est proche du début du trajet, où le vélo va lentement, et un autre point est proche du point d'arrivée où le vélo va vite.

Calculer la vitesse moyenne Étape 10 Étape 5. Testez la théorie intuitive
Utilisez le tableau ci-dessus pour déterminer la vitesse à différents moments. Certaines paires qui répondent à nos critères sont (t=0, t=5), (t=1, t=4), ou (t=2, t=3). Vous pouvez également tester cette formule avec des valeurs t autres que des entiers, si vous le souhaitez.
Quelle que soit la paire de points que vous choisissez, la vitesse moyenne à ce moment-là sera toujours la même. Par exemple, ((5+15)/2), ((7+13)/2) ou ((9+11)/2) sont tous égaux à 10 mètres/sec vers la droite

Calculer la vitesse moyenne Étape 11 Étape 6. Complétez l'explication intuitive
Si nous utilisons cette méthode avec une liste de chaque temps pris, nous continuerons à calculer la moyenne de la première moitié du voyage et de la seconde moitié du voyage. Le temps qu'il faut pour couvrir chaque moitié est le même, donc aucune vitesse n'est perdue lorsque nous avons fini de compter.
- Étant donné que l'une ou l'autre paire donnera le même résultat, la moyenne de ces vitesses sera également la même en valeur. Dans notre exemple, la vitesse de l'ensemble est de "10 mètres/sec vers la droite" sera toujours de 10 mètres/sec vers la droite.
- Nous pouvons trouver cette valeur en calculant la moyenne de n'importe quelle paire, par exemple les vitesses initiale et finale. Dans notre exemple, ces vitesses sont atteintes à t=0 et t=5, et peuvent être calculées à l'aide de la formule ci-dessus: (5+15)/2 = 10 mètres/sec vers la droite.

Calculer la vitesse moyenne Étape 12 Étape 7. Comprenez cette formule mathématiquement
Si vous êtes plus à l'aise avec les preuves écrites sous forme de formules, vous pouvez commencer par une formule pour calculer la distance parcourue en supposant une accélération constante, et en dériver la formule:
- s = vjet + à2. (Techniquement s et t, ou changement de position et changement dans le temps, mais vous seriez aussi compris si vous écriviez s et t.)
- Vitesse moyenne vun V défini comme s/t, entrez donc la formule sous la forme s/t.
- vun V = s/t = vje + à
- Accélération x temps est égal au changement de vitesse totale, ou vF -vje. Nous pouvons donc remplacer "at" dans la formule et obtenir:
- vun V = vje + (vF -vje).
- Simplifier: vun V = vje + vF -vje = vje + vF = (vF +vje)/2.
Des astuces
- La vitesse est différente de la vitesse car la vitesse est une quantité vectorielle alors que la vitesse est une quantité scalaire. Les quantités vectorielles impliquent à la fois la direction et la magnitude, tandis que les quantités scalaires n'impliquent que la magnitude.
- Si l'objet se déplace dans une dimension, telle que gauche-droite, vous pouvez utiliser un nombre positif pour représenter une direction (par exemple droite) et un nombre négatif pour représenter une autre direction (gauche). Écrivez cette notation en haut de votre page afin qu'elle soit claire pour les personnes qui lisent votre travail.






