3 façons de calculer l'aire d'un losange

Table des matières:

3 façons de calculer l'aire d'un losange
3 façons de calculer l'aire d'un losange

Vidéo: 3 façons de calculer l'aire d'un losange

Vidéo: 3 façons de calculer l'aire d'un losange
Vidéo: Chiffres ROMAINS - Savoir les ECRIRE et les LIRE - METHODE DIRECTE 2024, Peut
Anonim

Un losange est un quadrilatère à quatre côtés égaux. Il existe trois formules pour trouver l'aire d'un losange. Suivez simplement ces étapes pour savoir comment.

Étape

Méthode 1 sur 3: Utilisation de la diagonale

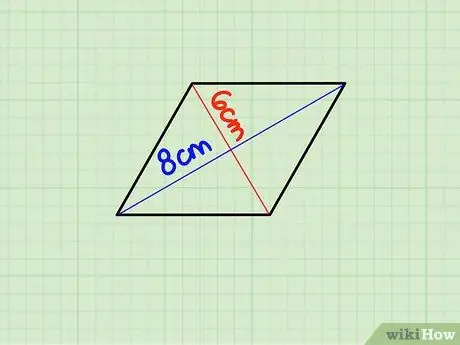
Calculer l'aire d'un losange Étape 1
Calculer l'aire d'un losange Étape 1

Étape 1. Trouvez la longueur de chaque diagonale

Les diagonales d'un losange sont des lignes reliant des sommets opposés (coins) au centre de la forme. Les diagonales d'un losange sont perpendiculaires et forment quatre triangles rectangles passant par le point d'intersection.

Disons que la diagonale est de 6 cm et la longueur est de 8 cm

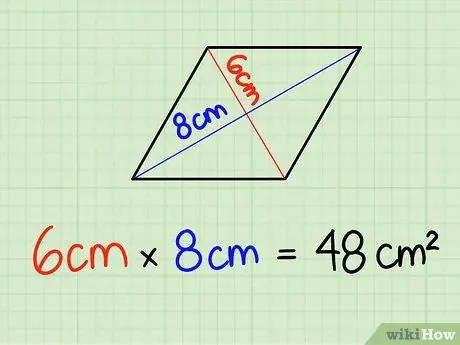
Calculer l'aire d'un losange Étape 2
Calculer l'aire d'un losange Étape 2

Étape 2. Multipliez la longueur de la diagonale

Notez simplement la longueur de la diagonale et multipliez. Dans ce cas, 6 cm x 8 cm = 48 cm2. N'oubliez pas de multiplier les unités car nous travaillons avec des unités carrées.

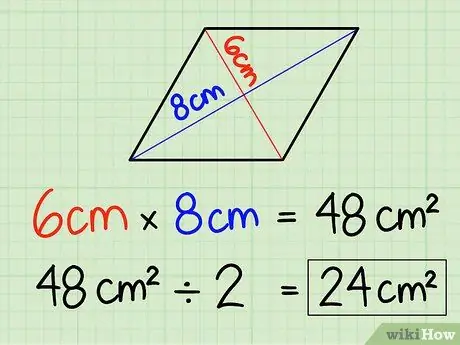
Calculer l'aire d'un losange Étape 3
Calculer l'aire d'un losange Étape 3

Étape 3. Divisez le résultat par 2

Parce que 6 cm x 8 cm = 48 cm2, il suffit de diviser le résultat par 2,48 cm2/2 = 24cm2. L'aire d'un losange est de 24 cm2.

Méthode 2 sur 3: Utilisation de la base et de la hauteur

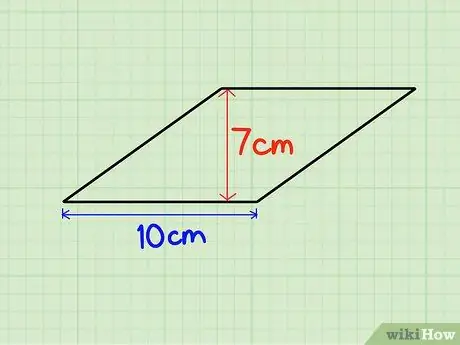
Calculer l'aire d'un losange Étape 4
Calculer l'aire d'un losange Étape 4

Étape 1. Trouvez la base et la hauteur

On peut aussi multiplier la hauteur du losange par la longueur du côté du losange. Disons que la hauteur du losange est de 7 cm et la base est de 10 cm.

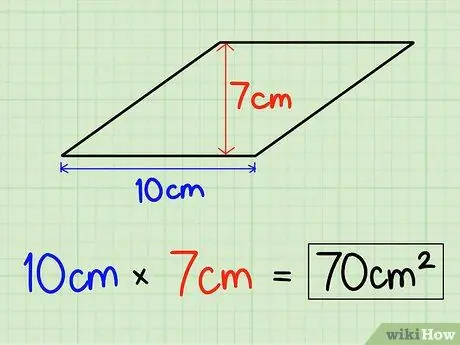
Calculer l'aire d'un losange Étape 5
Calculer l'aire d'un losange Étape 5

Étape 2. Multipliez la base et la hauteur

Après avoir connu la base et la hauteur du losange, trouvez l'aire de la forme en la multipliant. Donc 10 cm x 7 cm = 70 cm2. L'aire d'un losange est de 70 cm2.

Méthode 3 sur 3: Utilisation de la trigonométrie

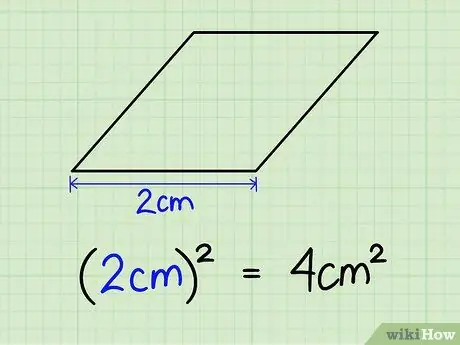
Calculer l'aire d'un losange Étape 6
Calculer l'aire d'un losange Étape 6

Étape 1. Équerre la longueur de n'importe quel côté

Un losange a quatre côtés égaux, donc peu importe le côté que nous choisissons. Disons que le côté a une longueur de 2 cm. 2cm x 2cm = 4cm2.

Calculer l'aire d'un losange Étape 7
Calculer l'aire d'un losange Étape 7

Étape 2. Multipliez par le sinus d'un coin

Peu importe l'angle que nous choisissons. Disons que l'un des angles est de 33 degrés. Il suffit de multiplier le sinus (33) par 4 cm2 pour obtenir l'aire du losange. (2cm)2 x sinus (33) = 4 cm2 x 1 = 4 cm2. L'aire d'un losange est de 4 cm2.

Conseillé:

4 façons de calculer l'aire d'un triangle

4 façons de calculer l'aire d'un triangle

La façon la plus courante de trouver l'aire d'un triangle est de diviser par deux le produit de la base et de la hauteur. Cependant, il existe également d'autres formules qui peuvent être utilisées en fonction des données connues. L'utilisation de données sur l'hypoténuse et l'angle d'un triangle, par exemple, peut vous permettre de calculer l'aire d'un triangle sans avoir besoin de connaître sa hauteur.

4 façons de calculer l'aire d'un cercle

4 façons de calculer l'aire d'un cercle

L'un des problèmes couramment rencontrés dans les cours de géométrie est le calcul de l'aire d'un cercle à partir des informations disponibles. Vous devez connaître la formule pour calculer l'aire d'un cercle, A=πr2{displaystyle A=\pi r^{2}} .

7 façons de calculer l'aire d'une forme plate

7 façons de calculer l'aire d'une forme plate

Il existe de nombreuses formes différentes de formes plates et il existe de nombreuses raisons pour lesquelles vous voudrez peut-être calculer une surface: des devoirs à l'estimation de la quantité de peinture nécessaire pour repeindre un salon.

3 façons de calculer l'aire d'un rectangle

3 façons de calculer l'aire d'un rectangle

Un rectangle est un quadrilatère dont deux côtés ont la même longueur, les deux autres côtés ont la même largeur et contiennent quatre angles droits. Pour trouver l'aire d'un rectangle on multiplie simplement la longueur par la largeur. Pour savoir comment trouver l'aire d'un rectangle, suivez ces étapes simples.

4 façons de calculer l'aire d'un hexagone

4 façons de calculer l'aire d'un hexagone

Un hexagone est un polygone qui a six côtés et angles. Un hexagone régulier a six côtés et angles égaux et se compose de six triangles équilatéraux. Il existe différentes manières de calculer l'aire d'un hexagone, qu'il s'agisse d'un hexagone régulier ou d'un hexagone irrégulier.