- Auteur Jason Gerald [email protected].
- Public 2023-12-16 11:11.
- Dernière modifié 2025-01-23 12:18.
La racine carrée d'un nombre est facile à trouver si la réponse est un nombre entier. Si la réponse n'est pas un nombre entier, il existe une série de processus que vous pouvez suivre pour obtenir la racine carrée, même si vous n'utilisez pas de calculatrice. Pour cela, vous devez comprendre les bases de la multiplication, de l'addition et de la division.
Étape
Méthode 1 sur 3: Trouver la racine carrée d'un entier
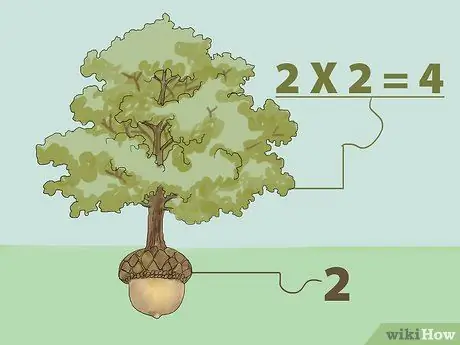
Étape 1. Trouvez la racine carrée parfaite en multipliant
La racine carrée d'un nombre est un nombre qui, multiplié par lui-même, renvoie le nombre d'origine. En d'autres termes: « Quel nombre pouvons-nous multiplier par lui-même pour obtenir le nombre que nous voulons ?
- Par exemple, la racine carrée de 1 est 1 car 1 multiplié par 1 est 1 (1X1=1). Ainsi, la racine carrée de 4 est 2 car 2 multiplié par 2 est 4 (2X2=4). Considérez le concept de racine carrée comme un arbre. Un arbre pousse à partir de graines. Ainsi, un arbre est plus gros qu'une graine, qui pousse à partir d'une graine qui est sa racine. Dans l'exemple ci-dessus, 4 est l'arbre et 2 est la graine.
- Ainsi, la racine carrée de 9 est 3 (3X3=9), de 16 est 4 (4X4=16), de 25 est 5 (5X5=25), de 36 est 6 (6X6=36), de 49 est 7 (7X7 =49), de 64 est 8 (8X8=64), de 81 est 9 (9X9=81), et de 100 est 10 (10X10=100).
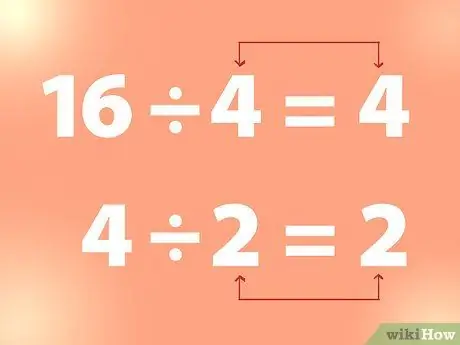
Étape 2. Utilisez la division continue pour trouver la racine carrée
Pour trouver la racine carrée d'un entier, vous pouvez diviser l'entier par un nombre jusqu'à ce que vous obteniez un nombre égal au diviseur.
- Exemple: 16 divisé par 4 fait 4. Et 4 divisé par 2 fait 2, et ainsi de suite. Ainsi, à partir de l'exemple ci-dessus, 4 est la racine carrée de 16 et 2 est la racine carrée de 4.
- Les racines carrées parfaites n'ont pas de fractions ou de décimales car ce sont des nombres entiers.
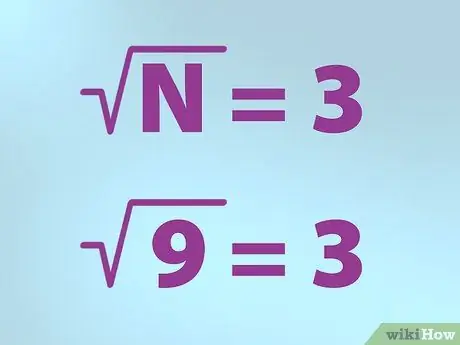
Étape 3. Utilisez le bon symbole pour la racine carrée
Les mathématiciens utilisent un symbole spécial pour représenter la racine carrée. La forme ressemble à une coche avec plus une ligne en haut à droite.
- N est égal au nombre dont vous voulez trouver la racine carrée. N est placé sous la coche.
- Donc, si vous voulez trouver la racine carrée de 9, écrivez une formule en mettant "N" (9) à l'intérieur d'une coche (symbole "racine") puis écrivez un signe égal et suivi de 3. Cela signifie "racine carrée de 9 est égal à 3".
Méthode 2 sur 3: Trouver la racine carrée d'un autre nombre
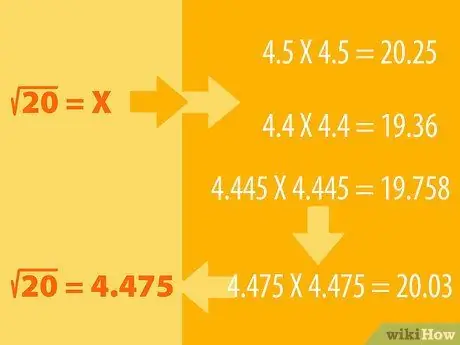
Étape 1. Devinez et effectuez le processus d'élimination
Il est difficile de trouver la racine carrée d'un nombre non entier. Cependant, cela ne veut pas dire que c'est impossible.
- Par exemple, disons que vous voulez trouver la racine carrée de 20. Nous savons que 16 est un carré parfait dont la racine carrée est 4 (4X4=16). Alors les 25 racines carrées sont 5 (5X5=25), donc la racine carrée de 20 doit se situer entre les deux.
- Vous pouvez deviner que la racine carrée de 20 est 4,5. Maintenant, carré 4,5 pour voir le résultat. C'est-à-dire que nous multiplions 4, 5 par lui-même: 4, 5X4, 5. Voyez si la réponse est supérieure ou inférieure à 20. Si votre estimation est trop éloignée, essayez un autre nombre (par exemple 4, 6 ou 4, 4) et ajustez devinez en conséquence jusqu'à ce que vous obteniez le nombre 20.
- Par exemple, 4, 5X4, 5 = 20, 25, donc logiquement nous devons trouver un nombre plus petit, peut-être 4, 4. 4, 4X4, 4 = 19, 36. Donc, la racine carrée de 20 doit se situer entre 4, 5 et 4, 4. Essayez avec 4, 445X4, 445. Le résultat est 19, 758. Le résultat se rapproche. Continuez d'essayer avec d'autres nombres jusqu'à ce que vous obteniez 4, 475X4, 475 = 20, 03. Arrondi, ce nombre est égal à 20.

Étape 2. Utilisez le processus de moyenne
Ce processus commence également par trouver les deux carrés parfaits les plus proches qui sont flanqués du nombre.
- Divisez ensuite ce nombre par l'une des racines carrées parfaites. Prenez la réponse, puis trouvez la moyenne entre ce nombre et le nombre dont vous voulez trouver la racine (vous pouvez trouver la moyenne en additionnant les deux et en divisant par deux). Divisez ensuite le nombre initial par la moyenne obtenue. La dernière étape, trouver la moyenne des résultats avec la moyenne calculée la première fois.
- Cela vous semble compliqué ? Ce serait plus simple si on donnait un exemple. Par exemple, 10 se situe entre les deux carrés parfaits 9 (3X3=9) et 16 (4X4=16). Les racines carrées des deux nombres sont 3 et 4. Donc, divisez 10 par le premier nombre, 3. Le résultat est 3, 33. Trouvez maintenant la moyenne de 3 et 3, 33 en les additionnant et en divisant par 2. Le résultat est 3, 1667 Maintenant, divisez 10 par 3,1667. Le résultat est 3,1579. Trouvez ensuite la moyenne de 3,1579 et 3,1667 en les additionnant et en divisant par 2. Le résultat est 3,1623.
- Vérifiez votre résultat en multipliant la réponse (dans cet exemple 3, 1623) par elle-même. Le résultat de 3,1623 multiplié par 3,1623 s'avère être 10,001.
Méthode 3 sur 3: Mise au carré des nombres négatifs
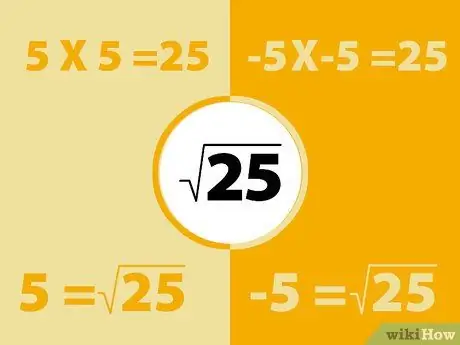
Étape 1. Placer des nombres négatifs au carré en utilisant la même méthode
N'oubliez pas que négatif fois négatif est positif. Ainsi, le carré d'un nombre négatif produira un nombre positif.
- Par exemple, -5X-5 = 25. Cependant, n'oubliez pas que 5x5=25. Ainsi, la racine carrée de 25 peut être -5 ou 5. Fondamentalement, chaque nombre a deux racines carrées.
- De même, 3X3=9 et -3X-3=9, donc les racines carrées de 9 sont 3 et -3. La racine carrée positive est appelée "racine principale". À ce stade, nous devons juste faire attention à cette réponse.
Étape 2. Utilisez une calculatrice
Bien qu'il soit préférable de pouvoir faire les calculs à la main, il existe de nombreuses calculatrices en ligne disponibles pour calculer les racines carrées.
- Recherchez le bouton racine carrée sur une calculatrice ordinaire.
- Dans la calculatrice en ligne, entrez directement le nombre dont vous souhaitez trouver la valeur de racine carrée et cliquez sur le bouton. L'ordinateur vous montrera la valeur de la racine carrée.
Des astuces
-
Gardez toujours à l'esprit quelques carrés parfaits importants:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Souvenez-vous aussi de ce carré parfait: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Notez également ceci: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






