- Auteur Jason Gerald [email protected].
- Public 2024-01-15 08:14.
- Dernière modifié 2025-01-23 12:18.
Il y a plusieurs façons de faire la division. Vous pouvez diviser des décimales, des fractions ou même des exposants et utiliser une division longue ou courte. Si vous voulez connaître les différentes façons de diviser les nombres, suivez les étapes ci-dessous.
Étape
Méthode 1 sur 5: Effectuer une division en série longue

Étape 1. Notez les questions
Pour effectuer une division longue, placez le dénominateur (le nombre qui divisera) à l'extérieur de la barre du diviseur et le numérateur (le nombre à diviser) à l'intérieur de la barre du diviseur.
Par exemple: 136÷3

Étape 2. Divisez le premier chiffre du numérateur par le dénominateur (si possible)
Dans cet exemple, 1 n'est pas divisible par 3, alors mettez un 0 au-dessus de la barre du diviseur et passez à l'étape suivante. Soustrayez 1 par 0 et placez le résultat sous le nombre 1.

Étape 3. Divisez le nombre du reste du premier chiffre du numérateur et du deuxième chiffre du numérateur par le dénominateur
Comme 1 ne peut pas être divisé par 3, le nombre 1 est toujours utilisé. Vous devez soustraire 3. Maintenant, divisez 13 par 3. Puisque 3 x 4 = 12, placez le 4 au-dessus de la barre du diviseur (à droite de 0), puis soustrayez 13 par 12 et écrivez le résultat en dessous.

Étape 4. Divisez les nombres restants par le dénominateur
Abaissez le nombre 6 à droite de 1, pour obtenir 16. Maintenant, divisez 16 par 3. Puisque 3 x 5 = 15, écrivez le nombre 5 à droite du nombre 4, et soustrayez 16 par 15 et écrivez le résultat (16-15= 1) en dessous.

Étape 5. Écrivez le reste à côté du quotient
Votre réponse finale est 45 avec 1 restant, ou 45 R1.
Méthode 2 sur 5: Effectuer des divisions courtes

Étape 1. Notez les questions
Écrivez le dénominateur (le nombre à diviser) à l'extérieur de la barre du diviseur et le numérateur (le nombre à diviser) à l'intérieur de la barre du diviseur. Notez que dans la division courte, le dénominateur ne peut pas être plus d'un chiffre.
Par exemple, 518 4

Étape 2. Divisez le premier chiffre du numérateur par le dénominateur
5 4 = 1 R1. Placez le quotient (1) au-dessus de la longue barre de séparation. Écrivez le reste au-dessus du premier chiffre du numérateur. Placez un petit 1 sur 5 pour vous rappeler qu'il vous reste 1 lorsque vous divisez 5 par 4. Le 518 devrait maintenant ressembler à ceci: 5118

Étape 3. Divisez le nombre formé à partir du reste et du deuxième chiffre du numérateur par le dénominateur
Le nombre suivant est 11 qui est obtenu à partir de la valeur résiduelle (1) et du deuxième chiffre du numérateur (1). 11 4 = 2 R 3 car 4 x 2 = 8 avec un reste de 3. Écrivez la valeur résiduelle au-dessus du deuxième chiffre du numérateur. Mettez 3 sur 1. Le numérateur initial (518) ressemble maintenant à ceci: 51138

Étape 4. Divisez les nombres restants par le dénominateur
Le nombre restant est 38; le nombre 3 provient du reste de l'étape précédente, et 8 est le dernier chiffre du numérateur. Calculez 38 4 = 9 R2. Puisque 4 x 9 = 36, écrivez "R2" au-dessus de la barre de division car 38 - 36 = 2.

Étape 5. Écrivez la réponse finale
Le résultat final et le quotient sont au-dessus de la barre du diviseur. La réponse est 518 4 = 129 R2.
Méthode 3 sur 5: Diviser les fractions

Étape 1. Notez les questions
Pour diviser une fraction, écrivez simplement la première fraction suivie du symbole de division, puis de la deuxième fraction.
Par exemple: 3/4 5/8

Étape 2. Inversez le numérateur et le dénominateur de la deuxième fraction
La seconde fraction est maintenant réciproque.
Exemple: 3/4 8/5

Étape 3. Remplacez le symbole de division par le symbole de temps
Pour diviser une fraction, vous multipliez la première fraction par l'inverse de la seconde.
Exemple: 3/4 x 8/5
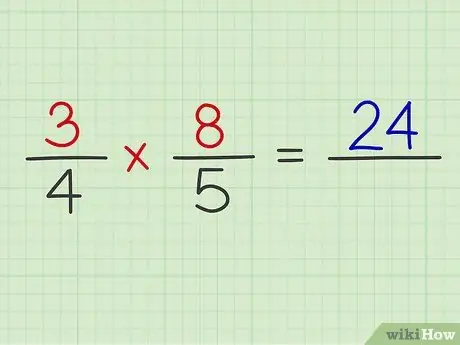
Étape 4. Multipliez le numérateur des deux fractions
Faites-le comme si vous multipliiez deux fractions régulières.
Exemple: 3 x 8 = 24
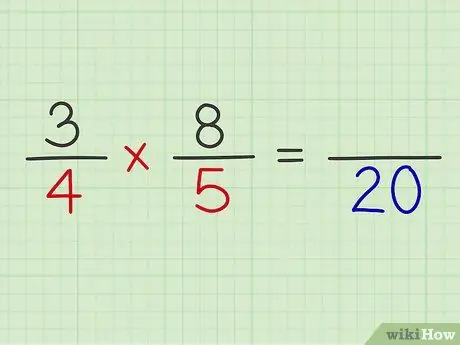
Étape 5. Multipliez les dénominateurs des deux fractions
Complétez le calcul en multipliant les deux fractions.
Exemple: 4 x 5 = 20
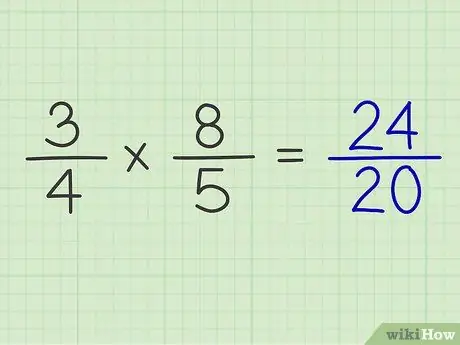
Étape 6. Mettez le produit du numérateur au-dessus du produit du dénominateur
Après avoir multiplié le numérateur et le dénominateur des deux fractions, vous pouvez obtenir le résultat du calcul des deux fractions.
Exemple: 3/4 x 8/5 = 24/20

Étape 7. Simplifiez les fractions
Pour trouver le plus grand facteur commun, ou le plus grand nombre qui divise également le numérateur et le dénominateur. Dans ce cas, le plus grand facteur commun de 24 et 20 est 4. Pour le prouver, notez tous les numérateurs et dénominateurs, et encerclez le nombre des plus grands facteurs communs des deux.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- Puisque 4 est le plus grand facteur commun de 24 et 20, il suffit de diviser les deux nombres par 4 pour simplifier la fraction.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Étape 8. Réécrivez la fraction sous forme de nombre mixte (facultatif)
L'astuce, il suffit de diviser le numérateur par le dénominateur et d'écrire le résultat sous la forme d'un nombre entier. Après cela, écrivez le reste de la division comme nouveau numérateur et le dénominateur de la fraction ne change pas. Puisque 6 divisé par 5 donne 1 avec un reste de 1, écrivez le nombre entier 1, suivi du nouveau numérateur 1, puis du dénominateur 5 pour obtenir un nombre mixte 1 1/5.
Exemple: 6/5 = 1 1/5
Méthode 4 sur 5: Diviser l'exposant

Étape 1. Assurez-vous que les exposants/puissances ont le même numéro de base
Vous ne pouvez diviser les exposants que s'ils ont le même nombre de base. Sinon, vous pouvez essayer de les manipuler jusqu'à ce que vous obteniez le même numéro de base.
Exemple: x8 X5

Étape 2. Soustrayez l'exposant
Vous pouvez simplement soustraire le premier exposant par le second. Ne vous occupez pas des nombres de base pour l'instant.
Exemple: 8 - 5 = 3
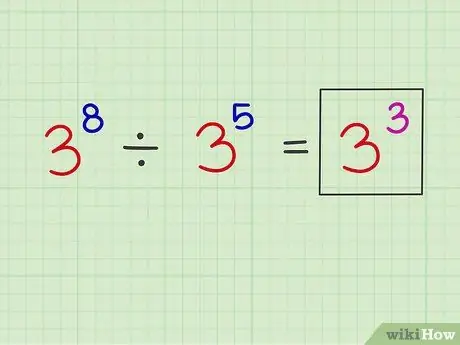
Étape 3. Placez le nouvel exposant au-dessus du nombre de base d'origine
Maintenant, vous pouvez écrire le nouvel exposant sur le nombre de base d'origine.
Exemple: x8 X5 = x3
Méthode 5 sur 5: Division de nombres décimaux

Étape 1. Notez les questions
Écrivez le dénominateur (le nombre à diviser) à l'extérieur de la barre du diviseur et le numérateur (le nombre à diviser) à l'intérieur de la barre du diviseur. Dans la division décimale, votre objectif est de convertir un nombre décimal en un nombre entier.
Exemple: 65,5.5

Étape 2. Remplacez le dénominateur par un nombre entier
Faites simplement glisser le point décimal d'un chiffre vers la droite pour changer 0,5 à 5, alias 5, 0.

Étape 3. Modifiez le numérateur en décalant le point décimal du même nombre de chiffres que le dénominateur
Étant donné que vous déplacez le point décimal du numérateur d'un chiffre vers la droite pour qu'il devienne un nombre entier, le point décimal du dénominateur est également décalé d'un chiffre vers la droite de sorte que 65,5 passe à 655.
Si vous décalez le point décimal du numérateur au-delà de tous ses chiffres, cela signifie que vous devez ajouter des zéros aux chiffres à chaque fois que le point décimal est décalé. Par exemple, si la virgule décimale 7, 2 est décalée de trois chiffres vers la droite, le nombre passe à 7 200 car l'espace vide à deux chiffres est rempli de zéros

Étape 4. Placez le point décimal sur la longue barre de division juste au-dessus du point décimal dans le numérateur
Puisque vous décalez la virgule d'un chiffre pour faire de 0,5 un nombre entier, c'est une bonne idée de placer la virgule au-dessus de la barre de division exactement là où la virgule est décalée, c'est-à-dire après les 5 derniers de 655.

Étape 5. Résolvez le problème avec une division longue simple
Pour diviser 655 par 5, les étapes sont:
- Divisez le chiffre des centaines du numérateur (6) par le dénominateur (5). Le résultat est 1 avec un reste de 1. Écrivez le nombre 1 au-dessus de la barre du diviseur, et écrivez 5 sous le nombre 6 à soustraire.
- Le reste de 1 est soustrait du chiffre des dizaines du numérateur (5) de sorte que vous obtenez maintenant 15. Divisez 15 par 5 pour obtenir 3. Écrivez 3 au-dessus de la barre du diviseur, à droite de 1.
- Supprimez les 5 derniers chiffres. Divisez 5 par 5 pour obtenir 1. Écrivez le chiffre 1 au-dessus de la barre du diviseur, à droite du chiffre 3. Il n'y a pas de reste car 5 est divisible par 5.
- La longue réponse de division séquentielle est 655 5 = 131. Ce résultat est le même que la réponse aux questions 65,5 0,5.






