- Auteur Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- Dernière modifié 2025-06-01 06:06.
La soustraction consiste simplement à soustraire un nombre à un autre. Il est facile de soustraire un nombre entier d'un autre, mais la soustraction peut être délicate si vous soustrayez des fractions ou des nombres décimaux. Une fois que vous aurez compris la soustraction, vous pourrez utiliser des concepts mathématiques plus complexes et pouvoir additionner, multiplier et diviser des nombres plus facilement.
Étape
Méthode 1 sur 6: Soustraire de grands nombres entiers en empruntant

Étape 1. Écrivez un grand nombre
Par exemple, vous voulez résoudre 32 - 17. Écrivez 32 d'abord.

Étape 2. Écrivez le plus petit nombre juste en dessous
Assurez-vous de placer les valeurs des dizaines et des unités dans les bonnes colonnes, de sorte que 3 sur 32 soit directement au-dessus de 1 sur 17 et que 2 sur 32 soit directement au-dessus de 7 sur 17.
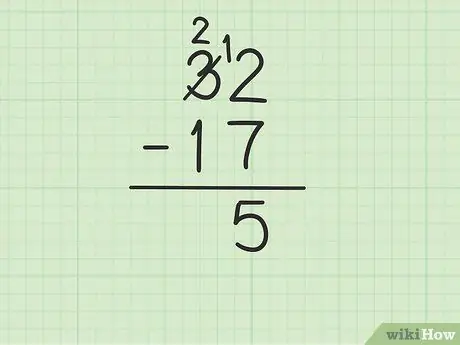
Étape 3. Soustrayez le nombre du haut de la colonne des unités du nombre du bas
Cependant, cela peut devenir compliqué si le nombre inférieur est supérieur au nombre supérieur. Dans ce cas, 7 est supérieur à 2. Voici ce que vous devez faire:
- Il faut emprunter au nombre 3 sur 32 (appelé aussi regroupement), pour transformer 2 en 12.
- Croisez le chiffre 3 sur 32 et remplacez-le par le chiffre 2, tandis que le chiffre 2 devient 12.
- Maintenant, vous pouvez soustraire 12 à 7, ce qui équivaut à 5. Écrivez 5 sous les deux nombres que vous soustrayez afin qu'ils soient dans la colonne des unités de la nouvelle ligne.
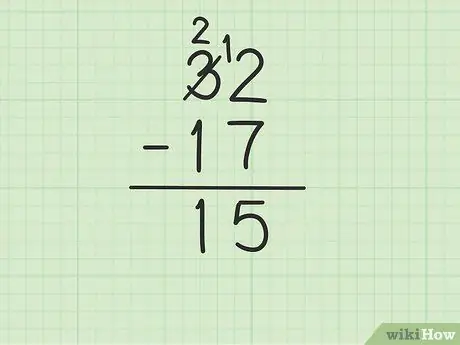
Étape 4. Soustrayez le nombre du haut de la colonne des dizaines du nombre du bas
Rappelez-vous que 3 est devenu 2. Maintenant, soustrayez 1 de 17 de 2 ci-dessus pour obtenir (2-1) 1. Écrivez 1 ci-dessous, dans la colonne des dizaines, à gauche de 5 dans la colonne des unités. Vous écrivez 15. C'est-à-dire 32 - 17 = 15.
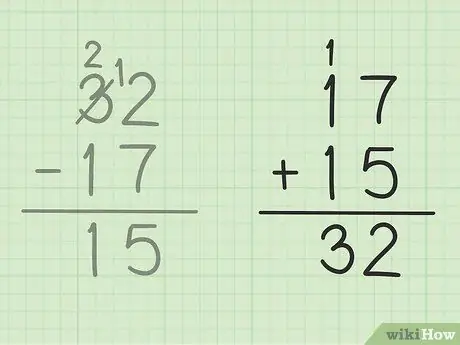
Étape 5. Vérifiez votre travail
Si vous voulez vous assurer que vous avez correctement soustrait deux nombres, alors tout ce que vous avez à faire est d'additionner votre réponse avec le plus petit nombre pour faire un grand nombre. Dans ce problème, vous devez ajouter votre réponse, 15 au plus petit nombre de soustraction, 17. 15 + 17 = 32, pour que votre réponse soit correcte. En sécurité!
Méthode 2 sur 6: Soustraire de petits nombres entiers
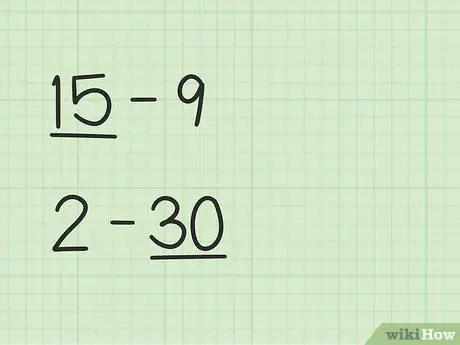
Étape 1. Trouvez le plus grand nombre
Des problèmes comme 15 -9 auront une manière différente de 2 - 30.
- Aux questions 15 à 9, le premier nombre, 15, est supérieur au deuxième nombre, 9.
- Aux questions 2 à 30, le deuxième nombre, 30, est supérieur au premier nombre, 2.
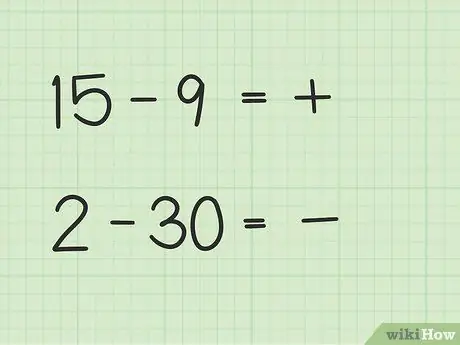
Étape 2. Décidez si votre réponse sera positive ou négative
Si le premier nombre est supérieur, la réponse est positive. Si le deuxième nombre est supérieur, la réponse est négative.
- À la première question, 15 - 9, votre réponse est positive car le premier nombre est supérieur au deuxième.
- À la deuxième question, 2 à 30, votre réponse est négative car le deuxième nombre est supérieur au premier.
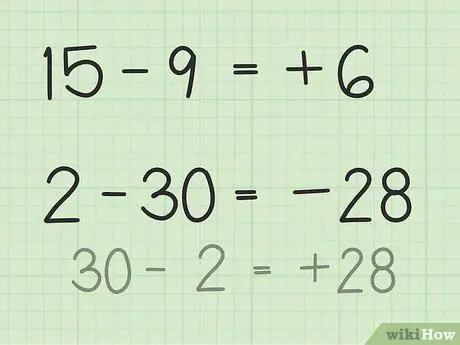
Étape 3. Trouvez la différence entre deux nombres
Pour soustraire deux nombres, vous devez imaginer la différence entre les deux nombres et calculer les nombres entre eux.
- Pour les questions 15 à 9, imaginez une pile de 15 jetons de poker. Jetez 9 jetons et seulement 6. Donc, 15 - 9 = 6. Vous pouvez aussi imaginer une droite numérique. Pensez aux nombres de 1 à 15, puis jetez ou retournez 9 unités pour obtenir 6.
- Pour les questions 2 à 30, la façon la plus simple de résoudre ce problème est d'inverser le nombre et de rendre le résultat négatif après soustraction. Donc, 30 - 2 = 28 donc 28 et 30 ont une différence de 2. Maintenant, rendez le résultat négatif car vous avez déjà déterminé que la réponse est négative car le deuxième nombre est supérieur au premier nombre. Donc, 2 - 30 = -28.
Méthode 3 sur 6: Soustraction de nombres décimaux
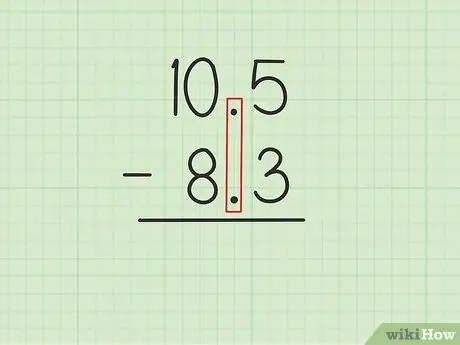
Étape 1. Écrivez le plus grand nombre sur le plus petit nombre avec les points décimaux alignés
Supposons que vous vouliez résoudre les problèmes suivants: 10, 5 - 8, 3. Écrivez 10, 5 sur 8, 3 pour que les décimales des deux nombres soient parallèles., 5 sur 10, 5 doit être directement au-dessus de, 3 sur 8, 3 et 0 sur 10, 5 doit être au-dessus de 8 sur 8, 3.
Si vous avez un problème parce que les deux nombres n'ont pas le même nombre après la virgule, écrivez 0 dans le blanc jusqu'à ce que la somme des nombres soit la même. Par exemple, le problème est 5, 32 - 4, 2, vous pouvez l'écrire comme 5, 32 - 4, 2 0. Cela ne changera pas la valeur du deuxième nombre, mais facilitera la soustraction des deux nombres.

Étape 2. Soustrayez le nombre du haut de la colonne des dizaines du nombre ci-dessous
Dans ce cas, vous devez soustraire 3 de 5. 5 - 3 = 2, vous devez donc écrire 2 sous 3 de 8, 3.
Assurez-vous de mettre un point décimal dans la réponse, de sorte qu'il soit écrit, 2

Étape 3. Soustrayez le nombre au-dessus de la colonne des unités du nombre en dessous
Vous devez soustraire 8 à 0. Empruntez 1 à la partie des dizaines pour changer 0 à 10 et soustrayez 10 à 8 pour obtenir 2. Vous pouvez également compter 10 à 8 sans emprunter car il n'y a pas de nombres dans la deuxième colonne des dizaines. Écrivez la réponse sous 8, à gauche de la virgule décimale.

Étape 4. Notez votre résultat final
Votre résultat final est 2, 2.

Étape 5. Vérifiez votre travail
Si vous voulez vous assurer que votre soustraction décimale est correcte, tout ce que vous avez à faire est d'additionner votre réponse avec le plus petit nombre pour obtenir le plus grand nombre. 2, 2 + 8, 3 = 10, 5, vous avez donc terminé.
Méthode 4 sur 6: Soustraire des fractions

Étape 1. Alignez le dénominateur et le numérateur de la fraction
Supposons que vous vouliez résoudre des problèmes 13/10 - 3/5. Écrivez le problème de sorte que les deux numérateurs 13 et 3 et les deux dénominateurs 10 et 5 soient opposés. Ces deux nombres sont séparés par un signe de soustraction. Cela vous aidera à visualiser le problème et à le résoudre plus facilement.

Étape 2. Trouvez le plus petit dénominateur commun
Le plus petit dénominateur commun est le plus petit nombre qui peut être divisé par deux nombres. Dans cet exemple, vous devez trouver le plus petit dénominateur commun qui est divisible par 10 et 5. Vous constaterez que 10 est le plus petit dénominateur commun pour les deux nombres car 10 est divisible par 10 et 5.
Notez que le plus petit dénominateur commun de deux nombres n'est pas toujours l'un d'entre eux. Par exemple, le plus petit dénominateur commun pour 3 et 2 est 6 car 6 est le plus petit nombre qui peut être divisé par deux nombres
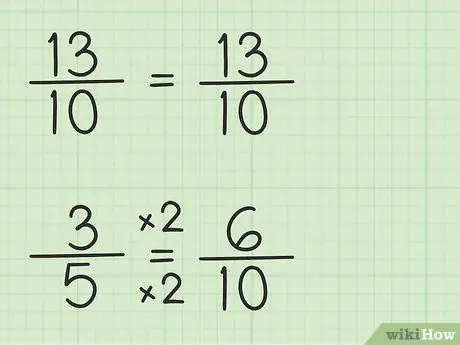
Étape 3. Écrivez les fractions en utilisant le même dénominateur
La fraction 13/10 peut s'écrire de la même manière car le dénominateur est 10, le plus petit dénominateur commun, qui est 10, fois 1. Cependant, la fraction 3/5 doit être réécrite car le dénominateur est 5, le plus petit dénominateur commun, qui est 10, fois 2. Donc la fraction 3/5 doit être multipliée par 2/2 pour faire le dénominateur 10, donc 3/5 x 2/2 = 6/10. Vous avez trouvé la fraction équivalente. 3/5 équivaut à 6/10 bien que 6/10 vous permette de soustraire le premier nombre, 13/10.
Écrivez une nouvelle question comme celle-ci: 13/10 - 6/10
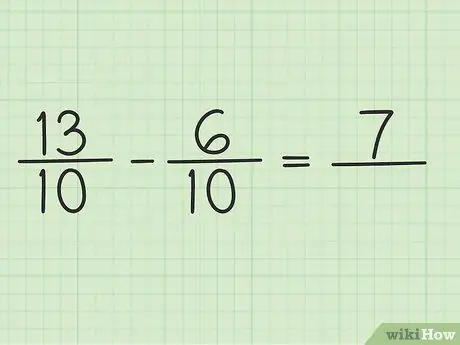
Étape 4. Soustrayez le numérateur à deux nombres
Il suffit de soustraire 13 à 6 pour que le résultat soit 7. Vous ne pouvez pas changer le dénominateur de la fraction.
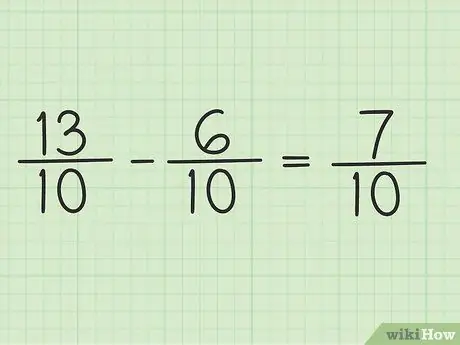
Étape 5. Écrivez le nouveau numérateur sur le même dénominateur pour obtenir le résultat final
Le nouveau numérateur est 7. Les deux fractions ont un dénominateur de 10. Votre résultat final est 7/10.
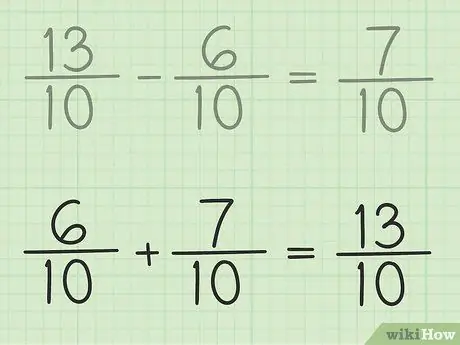
Étape 6. Vérifiez votre travail
Si vous voulez vous assurer que vous soustrayez correctement la fraction, additionnez simplement votre réponse et la fraction la plus petite pour que le résultat soit une fraction plus grande. 7/10 + 6/10 = 13/10. C'est fini.
Méthode 5 sur 6: Soustraire des fractions de nombres entiers

Étape 1. Notez le problème
Par exemple, supposons que vous vouliez résoudre le problème suivant: 5 -. Écris le.
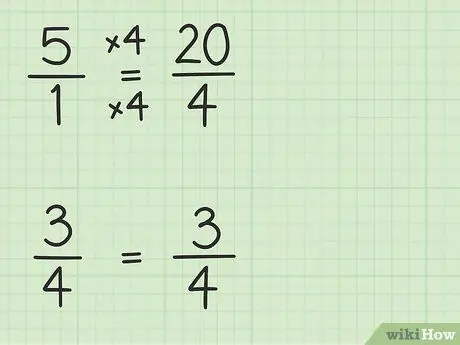
Étape 2. Convertissez des nombres entiers en fractions qui ont le même dénominateur que les autres fractions
Vous allez convertir 5 en fraction avec un dénominateur de 4 pour pouvoir soustraire deux nombres. Vous devez donc considérer 5 comme une fraction de 5/1. Ensuite, vous pouvez multiplier le numérateur et le dénominateur de la nouvelle fraction par 4 pour que les dénominateurs des deux nombres soient identiques. Donc 5/1 x 4/4 = 20/4. Cette fraction est égale à 5, mais permet de soustraire deux nombres.
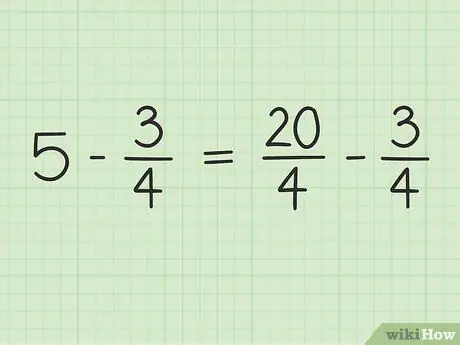
Étape 3. Réécrivez le problème
Le nouveau problème peut s'écrire ainsi: 20/4 - 3/4.
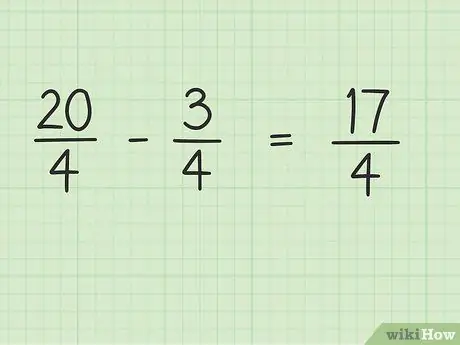
Étape 4. Soustrayez le numérateur de la fraction, tandis que le dénominateur reste le même
Maintenant, il suffit de soustraire 20 par 3 pour obtenir le résultat final. 20 - 3 = 17, donc 17 est le nouveau numérateur. Vous pouvez laisser le dénominateur le même.
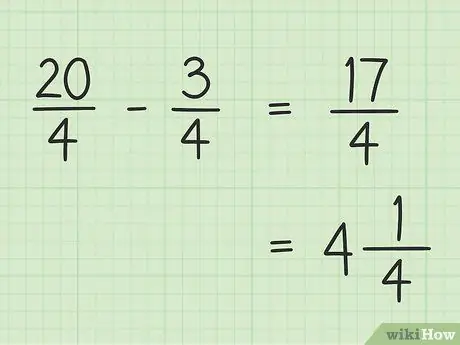
Étape 5. Notez votre résultat final
Votre résultat final est 17/4. Si vous voulez l'écrire sous forme de nombre mixte, divisez 17 par 4 pour que le résultat soit 4 et le reste soit 1, pour que votre 17/4 final soit égal à 4.
Méthode 6 sur 6: Soustraction de variables
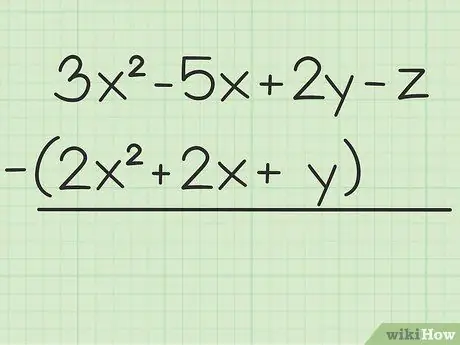
Étape 1. Notez le problème que vous souhaitez résoudre
Par exemple la question suivante: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Écrivez le premier ensemble de variables sur le second.
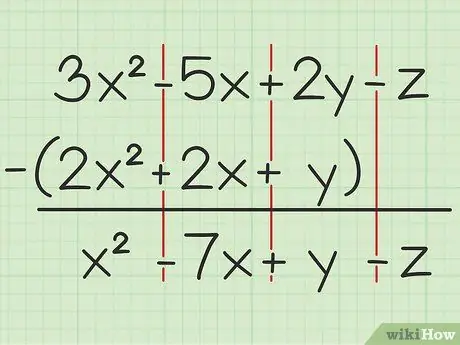
Étape 2. Soustrayez les mêmes variables
Si vous rencontrez une variable, vous ne pouvez qu'ajouter ou soustraire la même variable et qui s'écrit avec le même degré de carré. Cela signifie que vous pouvez soustraire 4x2 à partir de 7x2, mais ne peut pas soustraire 4x de 4y. Ainsi, vous pouvez décomposer le problème comme ceci:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
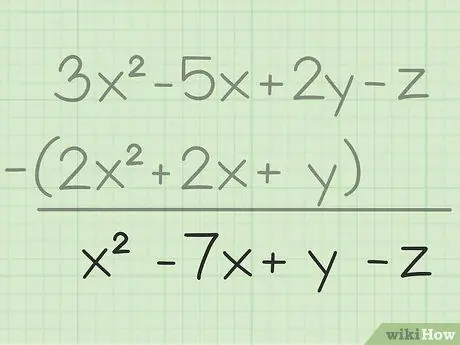
Étape 3. Notez votre résultat final
Vous avez soustrait toutes les mêmes variables, tout ce que vous avez à faire est d'écrire votre résultat final qui contiendra toutes les variables que vous avez soustraites. Voici le résultat final:






