- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:12.
- Dernière modifié 2025-01-23 12:18.
Les élèves encore très jeunes ont souvent du mal à comprendre le concept de soustraction. Si vous êtes enseignant et que vous souhaitez enseigner le concept de soustraction aux élèves, essayez de représenter le concept d'une manière intéressante et plus compréhensible pour les élèves. Après avoir expliqué les concepts de base de la soustraction, essayez de passer au concept de soustraction à deux chiffres. Une fois que les élèves l'ont bien maîtrisé, essayez d'expliquer divers concepts qu'ils peuvent utiliser pour résoudre des problèmes de soustraction, tels que Common Core.
Étape
Méthode 1 sur 4: Enseigner la soustraction à travers des objets ou des images

Étape 1. Écrivez ou présentez oralement un problème narratif contenant un problème de soustraction aux élèves:
Il y a 8 oranges sur la table, 3 oranges sont mangées par Jordan. Combien d'oranges reste-t-il ?
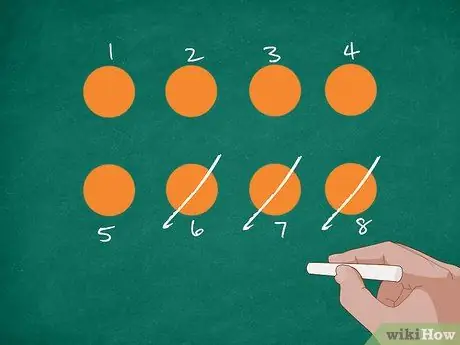
Étape 2. Représentez le problème avec des images
Tout d'abord, dessinez 8 cercles oranges au tableau ou sur une feuille de papier. Après cela, demandez aux élèves de compter le nombre et d'étiqueter chaque cercle avec un nombre. Rayez 3 cercles en expliquant que Jordan a mangé 3 oranges. Demandez aux élèves combien d'oranges il reste maintenant.
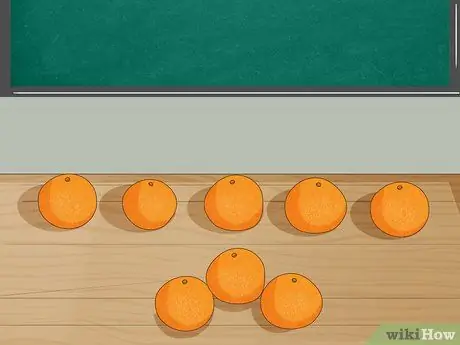
Étape 3. Représentez le problème avec des objets
Placez 8 oranges sur la table et demandez aux élèves de compter le nombre. Après cela, prenez 3 oranges sur la table en expliquant que Jordan a mangé 3 oranges. Demandez aux élèves de compter le nombre d'oranges restantes.

Étape 4. Écrivez l'équation
Expliquez que les problèmes de l'histoire peuvent également être représentés par une équation. Assurez-vous de toujours les guider dans le processus de transformation des problèmes de l'histoire en équations mathématiques.
- Demandez combien d'oranges sont sur la table. Écrivez le chiffre « 8 » au tableau.
- Demandez combien d'oranges Jordan a mangé. Écrivez le chiffre « 3 » au tableau.
- Demandez aux élèves s'il s'agit d'un problème d'addition ou de soustraction. Écrivez un signe « - » entre les chiffres « 8 » et « 3 ».
- Demandez aux élèves de chercher des réponses à l'équation « 8-3 ». Écrivez un signe "=" suivi du chiffre "5".
Méthode 2 sur 4: Enseigner la soustraction avec la méthode du compte à rebours sur la droite numérique

Étape 1. Écrivez ou présentez oralement un problème narratif contenant un problème de soustraction aux élèves:
Il y a 10 chiens dans l'animalerie, dont 6 ont été adoptés par leurs nouveaux propriétaires. Combien de chiens reste-t-il dans l'animalerie ?
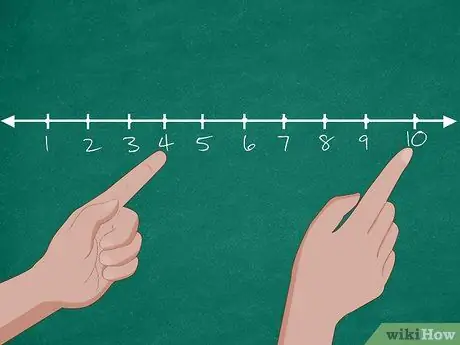
Étape 2. Utilisez l'aide d'une droite numérique pour résoudre le problème
Tout d'abord, tracez une droite numérique contenant les chiffres 0-10 au tableau. Après cela, demandez aux élèves de nommer le nombre de chiens dans l'animalerie. Une fois que les élèves ont répondu, encerclez le chiffre « 10 » au tableau. Ensuite, demandez à nouveau combien de chiens ont été adoptés. Si les élèves répondent « 6 », demandez-leur de compter 6 nombres à partir de 10 (9, 8, 7, 6, 5, 4) jusqu'à ce qu'ils atteignent le nombre « 4 ». Après cela, demandez à nouveau combien de chiens il reste à l'animalerie.

Étape 3. Écrivez l'équation
Expliquez que les problèmes de l'histoire peuvent également être représentés par une équation. Assurez-vous de toujours les guider dans le processus de transformation des problèmes de l'histoire en équations mathématiques.
- Demandez combien de chiens y a-t-il dans l'animalerie. Écrivez le nombre « 10 » au tableau.
- Demandez combien de chiens ont été adoptés. Écrivez le chiffre « 6 » au tableau.
- Demandez aux élèves s'il s'agit d'un problème d'addition ou de soustraction. Écrivez un signe « - » entre les chiffres « 10 » et « 6 ».
- Demandez aux élèves de chercher des réponses à l'équation « 10-6 ». Écrivez un signe "=" suivi du chiffre "4".
Méthode 3 sur 4: Enseigner la soustraction à l'aide de concepts de famille de faits

Étape 1. Présentez le concept de famille de faits aux élèves
En fait, une famille de faits est un groupe de problèmes mathématiques constitués des mêmes nombres. Par exemple, les nombres 10, 3 et 7 forment une famille de faits. Les trois nombres peuvent être additionnés ou soustraits de différentes manières; Vous pouvez générer deux équations en utilisant uniquement ces 3 nombres:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Étape 2. Écrivez ou présentez verbalement un problème d'histoire contenant un problème de soustraction aux élèves:
J'ai 7 bonbons. Si je mange 3 bonbons, combien reste-t-il de bonbons ?

Étape 3. Utilisez le concept de famille de faits pour résoudre le problème
Guidez les étudiants à travers le processus étape par étape:
- Demandez aux élèves quel problème ils aimeraient résoudre. Écrivez "7-3=?" sur le tableau noir.
- Demandez-leur d'identifier le troisième membre du groupe de famille de fait. Écrivez les équations suivantes au tableau: « 3+_=7 »; "_+3=7"; "; « 7-_=3 »; et 7-3=_ » Après cela, demandez aux élèves de lire les résultats et de compléter le problème avec les réponses qu'ils ont données.
Méthode 4 sur 4: Présentation des concepts de base communs
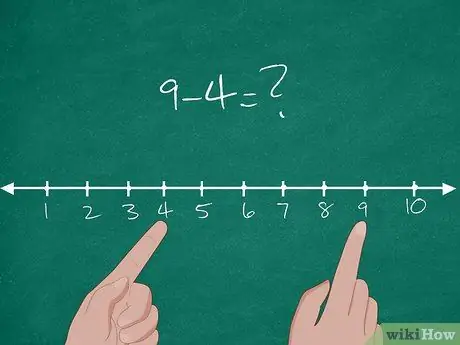
Étape 1. Enseignez le concept de soustraction dans Common Core
En fait, Common Core est une nouvelle norme d'apprentissage appliquée par la plupart des États américains. Dans Common Core, le concept de base de la soustraction s'explique par la distance entre deux nombres. Pour expliquer le concept aux élèves, essayez de tracer une droite numérique contenant les nombres 1 à 10 au tableau.
- Après cela, donnez un problème de soustraction de base aux élèves: 9-4=?.
- Trouvez l'emplacement du chiffre 4 sur la droite numérique. Expliquez aux élèves que cet endroit est leur point de départ.
- Trouvez l'emplacement du nombre 9 sur la droite numérique. Expliquez aux élèves que l'emplacement est la destination finale.
- Ensuite, demandez aux élèves de mesurer ou de calculer la distance entre les deux nombres: « 5, 6, 7, 8, 9 ».
- La distance entre les deux nombres est de 5. Ainsi, 9-4=5.
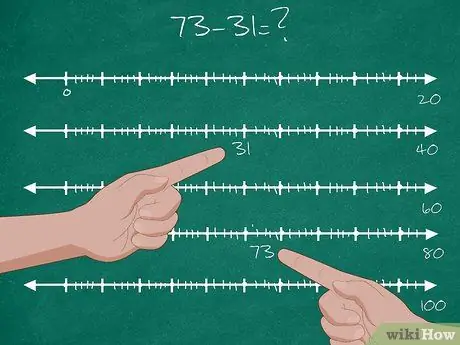
Étape 2. Demandez aux élèves de résoudre le problème de soustraction à deux chiffres
Expliquez aux élèves qu'il y aura deux points où ils devront s'arrêter avant d'arriver à destination.
- Donnez aux élèves un problème de soustraction à deux chiffres: 73-31=?.
- Trouvez l'emplacement du nombre 31 sur la droite numérique. C'est le point de départ.
- Trouvez l'emplacement du nombre 73 sur la droite numérique. C'est l'objectif final.
- « Stop » au premier dixième après le 31. Ainsi, votre premier arrêt est le 40. Après cela, mesurez la distance entre 31 et 40 et notez la réponse: 9.
- « Stop » aux dixièmes les plus proches de 73. Ainsi, votre deuxième arrêt est 70. Ensuite, mesurez la distance entre 40 (premier arrêt) et 70 (deuxième arrêt) et notez la réponse: 30.
- "Déplacez-vous" de 70 (deuxième arrêt) à votre destination finale (73). Mesurez la distance qui les sépare et notez la réponse: 3.
- Additionnez ces trois résultats: 9+30+3=42. Ainsi, 73-31=42.

Étape 3. Demandez aux élèves de résoudre le problème de soustraction à trois chiffres
Lors de la résolution de problèmes de soustraction à deux chiffres, expliquez aux élèves que ce qui augmentera, ce ne sont pas seulement les escales, mais aussi la distance entre chaque escale.
- Donnez aux élèves un problème de soustraction à trois chiffres: 815-398=?.
- Trouvez l'emplacement du nombre 398 sur la droite numérique. C'est le point de départ.
- Trouvez l'emplacement du nombre 815 sur la droite numérique. C'est l'objectif final.
- "Stop" au premier dixième après 398. Ainsi, votre premier stop est 400. Mesurez la distance entre 398 et 400, et notez la réponse: 2.
- « Stop » aux dixièmes les plus proches de 815. Votre deuxième arrêt est donc 800. Mesurez la distance entre 400 et 800 et notez la réponse: 400.
- « Stop » aux dixièmes les plus proches de 815. Ainsi, votre troisième arrêt est 810. Mesurez la distance entre 800 et 810 et notez la réponse: 10.
- « Déplacez-vous » du troisième arrêt jusqu'à votre destination finale, qui est le numéro 815. Mesurez la distance et notez la réponse: 5.
- Additionnez tous les nombres que vous obtenez: 2+400+10+5=417. Ainsi, 815-398-417.






