- Auteur Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- Dernière modifié 2025-06-01 06:06.
La valeur de position, ou le concept selon lequel la valeur d'un nombre (0-9) est déterminée par sa position dans un nombre particulier, est un concept fondamental en mathématiques. Étant donné que ce concept est si facile pour les personnes qui le comprennent déjà, l'enseigner peut être assez compliqué. Cependant, une fois que les étudiants auront compris ce concept, ils seront prêts et enthousiastes à utiliser leurs nouvelles compétences et à apprendre des concepts mathématiques plus complexes.
Étape
Partie 1 sur 3: Présentation des concepts de base

Étape 1. Prenez le temps d'enseigner la valeur de position
Si vous enseignez dans le cadre d'un programme prédéfini, vous devriez déjà avoir une idée de la manière d'intégrer la valeur de position dans un plus large éventail d'apprentissage. Si vous donnez des cours particuliers ou enseignez à domicile, la structure d'apprentissage sera plus flexible. Prévoyez d'enseigner la valeur de position quelque temps après que les élèves aient fini d'apprendre à compter et d'effectuer des opérations simples d'addition et de soustraction - généralement vers la première ou la deuxième année. Une compréhension de la valeur de position fournira à ces enfants une base pour comprendre des concepts mathématiques plus complexes.

Étape 2. Présentez le concept de comptage de groupes de nombres
La plupart des élèves des enfants n'apprennent qu'à compter les nombres un par un: un… deux… trois… quatre. C'est suffisant pour l'addition et la soustraction de base, mais encore trop simple pour fournir une base solide pour comprendre des fonctions plus complexes. Avant de leur apprendre à décomposer de grands nombres en leurs valeurs de position respectives, il est conseillé de leur apprendre à diviser un groupe de petits nombres en grands nombres.
- Apprenez à vos élèves à compter deux deux, trois trois, cinq cinq et dix dix. Il s'agit d'un concept fondamental que les élèves doivent comprendre avant d'apprendre la valeur de position.
- En particulier, essayez de créer un fort "frisson des dizaines". Les mathématiques modernes utilisent le nombre dix comme base, ce qui permet aux enfants d'apprendre plus facilement des systèmes plus complexes s'ils s'habituent à penser de cette façon. Apprenez à vos élèves à regrouper instinctivement les nombres en groupes de dix.

Étape 3. Revoyez le concept de valeur de position
Rafraîchissez votre compréhension. Assurez-vous de bien comprendre ce concept vous-même avant d'essayer de l'enseigner à un groupe de jeunes étudiants. En termes simples, la valeur de position est l'idée que la valeur d'un nombre (0-9) dépend de sa "place" ou de sa position dans un nombre.

Étape 4. Expliquez la différence entre les nombres et les nombres
Les nombres sont des symboles des dix nombres de base qui composent tous les nombres: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ces nombres sont combinés pour former tous les autres nombres. Un nombre peut être un nombre (par exemple le nombre 7), mais seulement s'il n'est pas groupé avec d'autres nombres. Lorsque deux nombres ou plus sont regroupés, la séquence des nombres forme le plus grand nombre.
Montrez que par lui-même "1" est le numéro un et "7" est le numéro sept. Lorsqu'ils sont regroupés en "17", les deux nombres forment le nombre dix-sept. De même, "3" et "5" forment ensemble le nombre trente-cinq. Montrez d'autres exemples pour que les élèves puissent rentrer chez eux en comprenant
Partie 2 sur 3: Enseignement par des exemples visuels
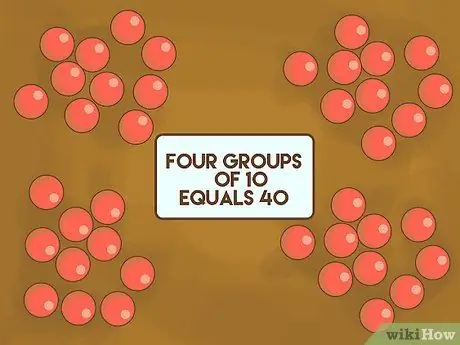
Étape 1. Montrez aux enfants qu'il est plus facile de compter de dix à dix
Utilisez 30 à 40 objets petits, dénombrables et assez homogènes. Par exemple: des cailloux, des billes ou une gomme. L'étaler sur la table devant les élèves. Expliquez qu'en mathématiques modernes, nous utilisons le nombre 10 comme base. Disposez les objets en plusieurs groupes, puis comptez-les devant la classe. Montrez-leur que quatre groupes de 10 cailloux font 40.

Étape 2. Traduisez l'exemple avec des cailloux en nombres écrits
Écrivez l'esquisse du concept au tableau. Tout d'abord, créez un graphique en T régulier. Écrivez le chiffre 1 dans le coin supérieur droit de la carte en T. Ensuite, écrivez le chiffre 10 dans le coin supérieur gauche. Écrivez un 0 dans la colonne de droite intitulée « 1 » et écrivez un 4 dans la colonne de gauche intitulée « 10 ». Vous pouvez maintenant expliquer à la classe que chaque numéro fait avec des cailloux a sa propre « place ».
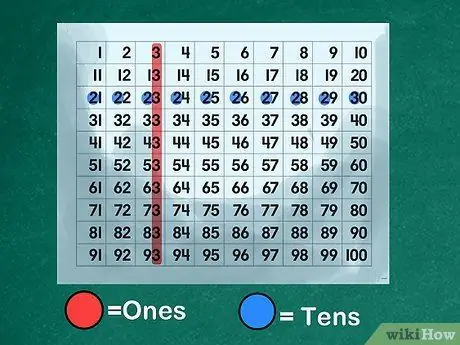
Étape 3. Utilisez un pavé numérique pour illustrer la base de la valeur de position
Créez ou imprimez un « pavé numérique » qui affiche tous les nombres dans l'ordre de 1 à 100. Montrez aux élèves comment les nombres de 0 à 9 interagissent avec les nombres de 10 à 100. Expliquez que chaque nombre de 10 à 99 est composé de deux chiffres., un un nombre à la place des "uns" et un autre nombre à la place des "dizaines". Montrez que le nombre « 4 » représente « quatre » lorsqu'il est à la place des « uns », mais sert de préfixe pour le nombre « 40 » lorsqu'il est à la place des « dizaines ».
- Illustrer la place des "unités". Demandez à la classe de nommer tous les nombres qui ont le chiffre « 3 » à la place des « uns »: 3, 13, 23, 33, 43, 53, 63, 73, 83, 93.
- Expliquez le lieu des "dizaines". Demandez aux élèves de désigner tous les nombres qui ont un « 2 » au lieu de « dizaines »: 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Expliquez que le « 3 » dans « 23 » est empilé au-dessus de " 20 " marqué du numéro " 2 ". Apprenez à vos enfants à lire le lieu « dizaines » comme déclencheur d'apprentissage.

Étape 4. Expérimentez avec d'autres outils d'enseignement visuels
Vous pouvez organiser des objets physiques ou les dessiner au tableau. Vous pouvez expliquer la valeur de position en utilisant des incréments de valeur monétaire, que les élèves ont peut-être déjà étudiés, pour les relier à des valeurs numériques mises à l'échelle. Pour une activité amusante et interactive, essayez d'utiliser les élèves eux-mêmes comme valeur de « groupe ».
La mémoire humaine est dominée par des choses visuelles, donc le concept de valeur de position est encore abstrait jusqu'à ce que vous puissiez le rendre visuel. Pendant ce temps, les symboles numériques eux-mêmes peuvent encore être abstraits pour les enfants ! Cherchez des façons d'encadrer les activités de comptage de groupe et de valeur de position afin qu'elles soient simples, tangibles et intuitives
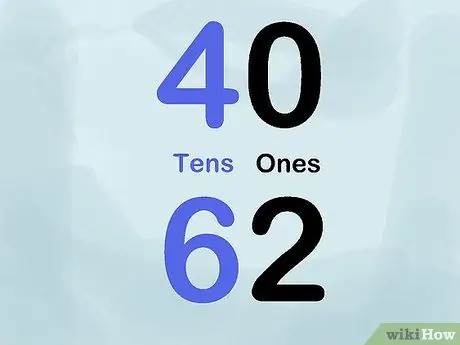
Étape 5. Utilisez la couleur
Essayez d'utiliser des craies ou des marqueurs de différentes couleurs pour démontrer la valeur de la position. Par exemple, écrivez divers nombres avec un marqueur noir pour la place « uns » et un marqueur bleu pour la place « dizaines ». Ainsi, vous écririez 40 avec le chiffre "4" en bleu et le chiffre "0" en noir. Répétez cette astuce pour un grand nombre de nombres pour montrer l'application de la valeur de position au tableau.
Partie 3 sur 3: Utiliser des exemples interactifs
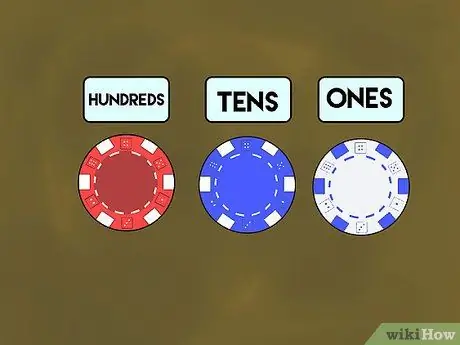
Étape 1. Enseignez avec des jetons de poker
Tout d'abord, distribuez les jetons de poker à chaque élève. Dites-leur que les jetons blancs représentent la place des « uns », les jetons bleus pour les « dizaines » et les jetons rouges représentent les « centaines ». Ensuite, montrez à vos élèves comment faire des nombres en utilisant des valeurs de position sous forme de jetons colorés. Nommez un nombre (disons 7) et placez la puce blanche à droite de votre bureau.
- Nommez un autre nombre - par exemple, 30. Mettez trois jetons bleus qui représentent 3 (à la place des « dizaines ») et zéro jeton blanc pour représenter 0 (à la place des « uns »).
- Vous n'êtes pas obligé d'utiliser des jetons de poker. Vous pouvez utiliser n'importe quel objet pour représenter les trois valeurs de "lieu" de base tant que chaque groupe (couleur de la puce, etc.) est standard, homogène et facilement reconnaissable.

Étape 2. Demandez aux élèves d'échanger des pièces entre eux
Cette méthode peut illustrer les valeurs de position basses qui composent les valeurs de position plus élevées. Une fois que les élèves ont démontré une bonne compréhension de la valeur de position, enseignez à votre classe comment échanger des jetons blancs « uns » contre des jetons bleus « dizaines », puis échanger des jetons « dizaines » contre des « centaines ». Demandez aux élèves: « Combien de jetons bleus est-ce que j'obtiens en échangeant 16 jetons blancs ? Si j'échange trois jetons bleus, combien de jetons blancs vais-je obtenir ? »

Étape 3. Montrez comment faire des additions et des soustractions avec des jetons de poker
Ce concept ne peut être enseigné qu'après que les étudiants aient maîtrisé l'échange de jetons de poker. Il est utile de commencer par écrire un exemple.
- Pour le problème d'addition de base, demandez aux élèves de poser trois jetons bleus (dizaines) et six jetons blancs (uns). Demandez aux élèves quels sont les nombres formés avec les jetons. (La réponse est 36 !)
- Continuez à travailler sur le même nombre. Demandez à vos élèves d'ajouter cinq jetons blancs au nombre 36. Demandez-leur quel est le nombre actuel. (La réponse est 41 !) Ensuite, prenez un jeton bleu et demandez-leur le numéro actuel. (La réponse est 31 !)






