L'IQR est l'intervalle interquartile ou l'intervalle racine du quartile d'un ensemble de données. L'IQR est utilisé dans l'analyse statistique pour aider à tirer des conclusions sur un ensemble de données. L'IQR est utilisé plus souvent que la plage car l'IQR n'inclut pas les données les plus externes. Continuez à lire pour apprendre à trouver l'IQR!
Étape
Méthode 1 sur 3: Comprendre l'IQR
Étape 1. Comprendre comment utiliser l'IQR
Fondamentalement, l'IQR est un moyen de comprendre la propagation d'un ensemble de nombres. La plage du quartile racine est définie comme la différence entre le quartile supérieur (25 % supérieur) et le quartile inférieur (25 % inférieur) de l'ensemble de données.
Conseil:
Le quartile inférieur est généralement écrit Q1 et le quartile supérieur Q3 – ce qui fait techniquement que le point médian des données est Q2 et le point le plus élevé Q4.
Étape 2. Comprendre les quartiles
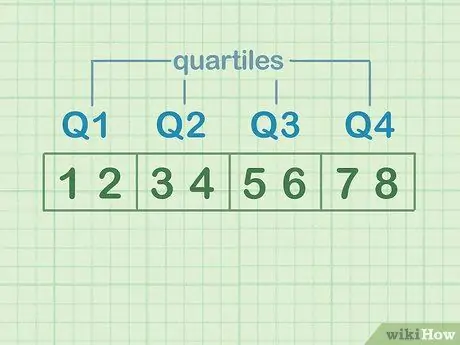
Pour illustrer les quartiles, divisez l'ensemble de nombres en quatre parties égales. Chacune de ces parties est un « quartile ». Supposons que les ensembles de données sont: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 et 2 sont le premier quartile ou Q1
- 3 et 4 sont le deuxième quartile ou Q2
- 5 et 6 sont le troisième quartile ou Q3
- 7 et 8 sont le quatrième quartile ou Q4
Étape 3. Apprenez la formule
Pour trouver la différence entre les quartiles supérieur et inférieur, vous devez soustraire le 75e centile du 25e centile.
La formule s'écrit: Q3 – Q1 = IQR
Méthode 2 sur 3: Compilation de l'ensemble de données
Étape 1. Collectez vos données
Si vous étudiez l'IQR en classe et dans les tests, vous recevrez peut-être un ensemble de données déjà préparé, par exemple 1, 4, 5, 7, 10. C'est votre ensemble de données - les nombres avec lesquels vous travaillerez. Cependant, vous pouvez créer vos propres nombres à partir de questions de table ou de problèmes d'histoire.
Assurez-vous que chaque nombre représente la même chose:
par exemple, le nombre d'œufs dans chaque nid d'une population d'oiseaux définie, ou le nombre de places de stationnement situées dans chaque maison dans un bloc spécifié.
Étape 2. Triez vos données par ordre croissant
En d'autres termes: arrangez les nombres du plus petit au plus grand. Utilisez les conseils des exemples suivants.
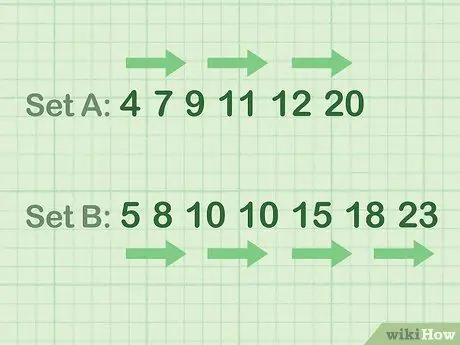
- Exemple de données de nombre pair (Set A): 4 7 9 11 12 20
- Exemple de données impaires (Set B): 5 8 10 10 15 18 23
Étape 3. Divisez les données en deux
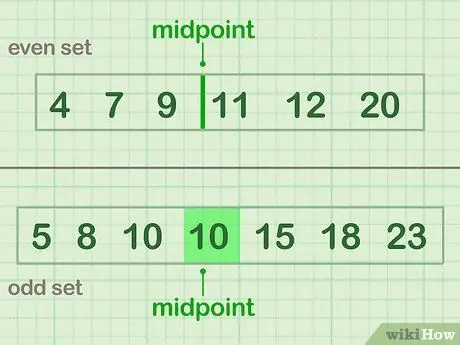
Pour diviser en deux, trouvez le milieu de vos données: le ou les nombres qui se trouvent au centre même de l'ensemble de données. Si vous avez un nombre impair de données, choisissez le nombre qui se trouve juste au milieu. Si vous avez un nombre pair de données, le point médian se situe entre les deux nombres les plus médians.
- Un exemple pair (Ensemble A) qui a un point médian entre 9 et 11: 4 7 9 | 11 12 20
- Un exemple étrange (Ensemble B) qui a une valeur médiane (10): 5 8 10 (10) 15 18 23
Méthode 3 sur 3: Calcul de l'IQR
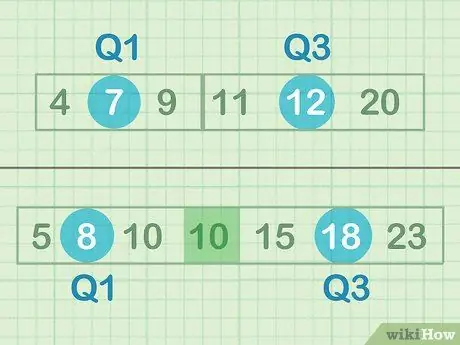
Étape 1. Trouvez la médiane de vos moitiés inférieure et supérieure des données
La médiane est le « point médian » ou le nombre qui se trouve au milieu d'un ensemble de nombres. Dans ce cas, vous ne recherchez pas le milieu de tous les nombres, mais le milieu relatif des sous-ensembles de données supérieur et inférieur. Si vous avez un nombre impair de données, n'incluez pas le nombre du milieu - par exemple, dans l'ensemble B, vous n'avez pas besoin d'inclure un seul 10.
-
Exemple pair (ensemble A):
- Médiane de la moitié inférieure des données = 7 (Q1)
- Médiane de la moitié supérieure des données = 12 (Q3)
-
Exemple étrange (ensemble B):
- Médiane de la moitié inférieure des données = 8 (Q1)
- Médiane de la moitié supérieure des données = 18 (Q3)
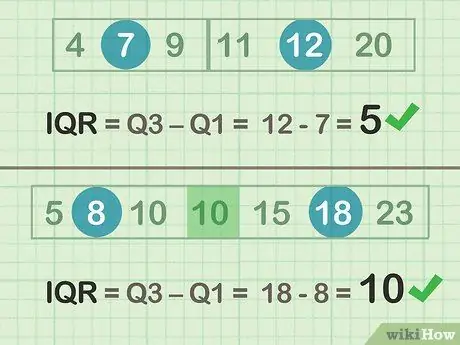
Étape 2. Soustrayez Q3-Q1 pour déterminer l'IQR
Vous savez maintenant combien de nombres se situent entre le 25e et le 75e centiles. Vous pouvez utiliser ce nombre pour comprendre la propagation d'une donnée. Par exemple, si un test a un score maximum de 100 et que l'IQR du score est de 5, vous pouvez supposer que la plupart des personnes qui passent le test ont presque la même compréhension car la plage des hauts et des bas n'est pas très large. Cependant, si l'IQR d'un test est de 30, vous pouvez commencer à vous demander pourquoi certaines personnes obtiennent des résultats si élevés et d'autres si bas.
- Exemple pair (ensemble A): 12 -7 = 5
- Exemple impair (ensemble B): 18 – 8 = 10
Des astuces
Il est important d'apprendre à le faire par vous-même. Cependant, il existe plusieurs calculatrices IQR en ligne que vous pouvez utiliser pour vérifier votre travail. Ne comptez pas trop sur les applications de calculatrice si vous apprenez cela en classe ! Si on vous demande de rechercher l'IQR dans un test, vous devrez savoir comment le trouver manuellement
WikiComment
- Comment détecter les valeurs aberrantes
- Comment calculer la plage d'un ensemble de données
- Comment faire un diagramme de boîte et de tente
