- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:14.
- Dernière modifié 2025-01-23 12:18.
La gravité est l'une des forces fondamentales de la physique. L'aspect le plus important de la gravité est qu'elle est universelle: tous les objets ont une force gravitationnelle qui attire d'autres objets. L'amplitude de la force gravitationnelle dépend de la masse et de la distance entre les deux objets.
Étape
Partie 1 sur 2: Calcul de la force de gravité entre deux objets

Étape 1. Définir l'équation de la force gravitationnelle tirant sur un objet, Fgrave = (Gm1m2)/ré2.
Pour pouvoir calculer la force gravitationnelle d'un objet, cette équation prend également en compte les masses des deux objets et leur distance l'un de l'autre. Les variables de l'équation sont décrites ci-dessous.
- Fgrave est la force gravitationnelle
- G est la constante gravitationnelle universelle 6,673 x 10-11 Nm2/kg2
- m1 est la masse du premier objet
- m2 est la masse du deuxième objet
- d est la distance entre les centres des deux objets
- Parfois, vous trouvez la lettre r au lieu de d. Ces deux symboles représentent la distance entre les deux objets.

Étape 2. Utilisez les unités métriques appropriées
Pour cette équation, vous devez utiliser des unités métriques. La masse de l'objet doit être en kilogrammes (kg) et la distance entre les objets doit être en mètres (m). Vous devez convertir ces unités en unités métriques avant de continuer

Étape 3. Déterminez la masse de l'objet en question
Pour les petits objets, vous pouvez les peser pour déterminer leur poids en kilogrammes. Pour les gros objets, vous pouvez rechercher la masse approximative sur une table ou sur Internet. Dans les problèmes de physique, la masse de l'objet sera généralement indiquée.

Étape 4. Mesurez la distance entre les deux objets
Si vous essayez de calculer la force gravitationnelle entre un objet et la Terre, vous devez savoir à quelle distance cet objet se trouve du centre de la Terre.
- La distance entre la surface de la terre et le centre de la terre est d'environ 6,38 x 106 m.
- Vous pouvez rechercher des tables ou d'autres sources sur Internet qui vous indiquent la distance approximative entre le centre de la Terre et des objets à différentes hauteurs sur la surface de la Terre.

Étape 5. Terminez le calcul
Si vous avez défini les variables dans l'équation, n'hésitez pas à les saisir pour résoudre. Assurez-vous que toutes les variables sont en unités métriques et sont correctement mises à l'échelle. La masse doit être en kilogrammes et la distance doit être en mètres. Résoudre des équations dans le bon ordre de calcul.
- Par exemple, déterminez la force gravitationnelle d'une personne dont la masse est de 68 kg au-dessus de la surface de la terre. La masse de la Terre est de 5,98 x 1024 kg.
- Assurez-vous que toutes les variables sont dans les bonnes unités. m1 = 5, 98x1024 kg, m2 = 68 kg, G = 6,673 x 10-11 Nm2/kg2, et d = 6, 38 x 106 m
- Écris ton équation: Fgrave = (Gm1m2)/ré2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)]/(6, 38 x 106)2
- Multipliez les masses des deux objets pris en compte. 68x (5, 98x1024) = 4,06 x 1026
- Multipliez le résultat m1 et M2 avec la constante gravitationnelle G. (4,06 x 1026) x (6,67 x 10-11) = 2 708 x 1016
- Carré la distance entre les deux objets. (6, 38 x 106)2 = 4,07 x 1013
- Partager le résultat G x m1 x m2 par la distance au carré pour obtenir la force gravitationnelle en Newtons (N). 2 708 x 1016/4, 07x1013 = 665N
- Sa force gravitationnelle est de 665 N.
Partie 2 sur 2: Calcul de la force de gravité sur Terre

Étape 1. Comprendre la deuxième loi de Newton, F = ma
La deuxième loi de Newton stipule que l'accélération d'un objet est directement proportionnelle à la force nette agissant sur lui et inversement proportionnelle à sa masse. En d'autres termes, si une force agissant sur un objet est supérieure à la force agissant dans la direction opposée, l'objet se déplacera avec la force la plus forte.
- Cette loi peut être résumée par l'équation F = ma, où F est la force, m est la masse de l'objet et a est l'accélération.
- Grâce à cette loi, nous pouvons calculer la force gravitationnelle de tous les objets à la surface de la Terre, en utilisant l'accélération connue due à la gravité.
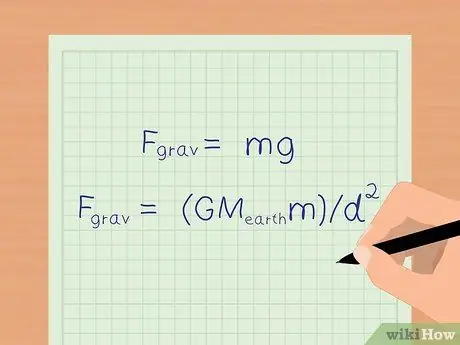
Étape 2. Trouvez l'accélération due à la gravité terrestre
Sur terre, la force de gravité fait accélérer tous les objets de 9,8 m/s2. A la surface de la terre, on peut utiliser une équation simplifiée: Fgrave = mg pour calculer la force gravitationnelle.
Si vous voulez connaître un nombre plus précis de forces gravitationnelles, vous pouvez toujours utiliser la formule de l'étape précédente, Fgrave = (GMTerreMaryland2 pour déterminer la force gravitationnelle.

Étape 3. Utilisez les unités métriques appropriées
Pour cette équation, vous devez utiliser des unités métriques. La masse de l'objet doit être en kilogrammes (kg) et la distance entre les objets doit être en mètres (m). Vous devez convertir ces unités en unités métriques avant de continuer.

Étape 4. Déterminez la masse de l'objet en question
Pour les petits objets, vous pouvez les peser pour déterminer leur poids en kilogrammes. Pour les gros objets, vous pouvez rechercher la masse approximative sur une table ou sur Internet. Dans les problèmes de physique, la masse de l'objet sera généralement indiquée.

Étape 5. Terminez le calcul
Si vous avez défini les variables dans l'équation, n'hésitez pas à les saisir pour résoudre. Assurez-vous que toutes les variables sont en unités métriques et sont correctement mises à l'échelle. La masse doit être en kilogrammes et la distance doit être en mètres. Résoudre des équations dans le bon ordre de calcul.
- Essayons d'utiliser l'équation de l'étape précédente et voyons à quel point les résultats sont proches. Déterminer la force gravitationnelle d'une personne d'une masse de 68 kg à la surface de la Terre.
- Assurez-vous que toutes les variables sont dans les bonnes unités: m = 68 kg, g = 9,8 m/s2.
- Écrivez la formule. Fgrave = mg = 68*9, 8 = 666 N.
- En utilisant la formule F = mg, la force gravitationnelle est de 666 N, tandis que le résultat de la formule de l'étape précédente est de 665 N. Comme vous pouvez le voir, les deux résultats sont presque les mêmes.
Des astuces
- Ces deux formules devraient donner la même réponse, mais la formule la plus courte et la plus simple est plus facile à utiliser lorsqu'on parle d'objets à la surface d'une planète.
- Utilisez la première formule si vous ne connaissez pas l'accélération due à la gravité sur une planète, ou si vous calculez la force gravitationnelle entre deux très gros objets, tels que la lune ou des planètes.






