- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:14.
- Dernière modifié 2025-06-01 06:06.
La force normale est l'amplitude de la force requise pour annuler les autres forces dans n'importe quel scénario. La meilleure façon de le trouver dépend de l'état de l'objet et des variables dont vous disposez. Continuez à lire pour en savoir plus.
Étape
Méthode 1 sur 5: Style normal au repos
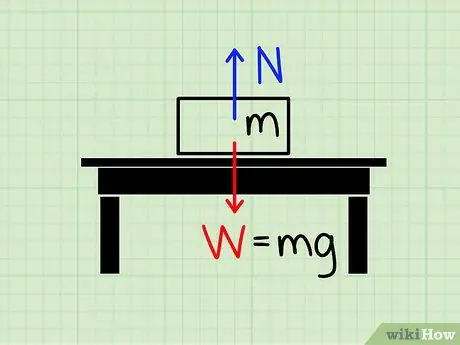
Étape 1. Comprendre la signification de la force normale
La force normale fait référence à l'amplitude de la force utilisée pour annuler la force gravitationnelle.
Imaginez un bloc au repos sur une table. La force de gravité tire le bloc vers la terre, mais clairement, il y a une force qui agit, empêchant le bloc d'écraser la table et de tomber au sol. La force qui agit pour arrêter ce bloc malgré la force de gravité est appelée style normal.
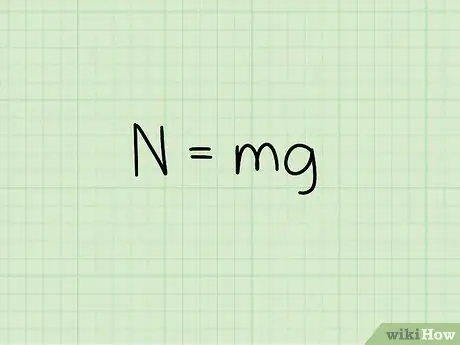
Étape 2. Connaître l'équation de la force normale sur un objet au repos
Lors du calcul de la force normale d'un objet lorsqu'il est au repos sur une surface plane, utilisez la formule: N = m * g
- Dans cette équation, N symbolise le style normal, m représente la masse de l'objet, et g représente l'accélération due à la pesanteur.
- Pour un objet au repos sur une surface plane, sans qu'une force externe agisse, la force normale est égale au poids de l'objet. Pour maintenir un objet au repos, la force normale doit être égale à la force gravitationnelle agissant sur l'objet. La force gravitationnelle agissant sur un objet est le poids de l'objet, ou la masse de l'objet multipliée par l'accélération due à la gravité.
- Exemple: Trouvez la force normale d'un bloc d'une masse de 4,2 kg.
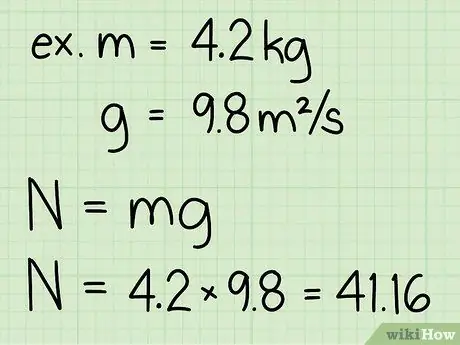
Étape 3. Multipliez la masse de l'objet et l'accélération due à la gravité
Cette multiplication produira le poids de l'objet, qui est bien sûr égal à la force normale de l'objet au repos.
- Notez que l'accélération due à la gravité à la surface de la terre est toujours constante: g = 9,8 m/s2
- Exemple: poids = m * g = 4, 2 * 9, 8 = 41, 16

Étape 4. Notez vos réponses
L'étape précédente résoudra le problème en vous donnant votre réponse.
Exemple: La force normale est de 41, 16 N
Méthode 2 sur 5: Force normale sur un plan incliné
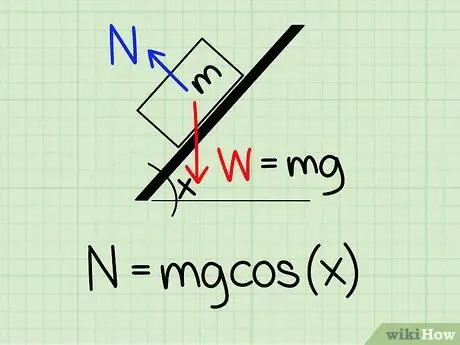
Étape 1. Utilisez la bonne équation
Pour calculer la force normale sur un objet incliné d'un certain angle, vous devez utiliser la formule: N = m * g * cos(x)
- Pour cette équation, N symbolise le style normal, m représente la masse de l'objet g représente l'accélération due à la gravité, et X représente l'angle oblique.
- Exemple: Trouvez la force normale d'un bloc d'une masse de 4,2 kg, qui repose sur un plan incliné avec une inclinaison de 45 degrés.

Étape 2. Trouvez le cosinus de l'angle
Le cosinus de l'angle est égal au sinus de l'angle complémentaire, ou au côté adjacent divisé par l'hypoténuse du triangle formé par la pente.
- Cette valeur est souvent déterminée avec une calculatrice car le cosinus de tout angle est toujours constant, mais vous pouvez également le calculer manuellement.
- Exemple: cos(45) = 0,71
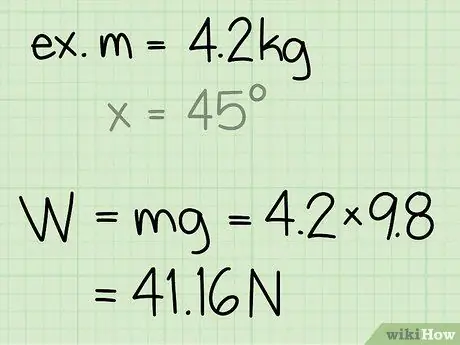
Étape 3. Trouvez le poids de l'objet
Le poids d'un objet est égal à la masse de l'objet multipliée par l'accélération due à la gravité.
- Notez que l'accélération due à la gravité à la surface de la terre est toujours constante: g = 9,8 m/s2
- Exemple: poids = m * g = 4, 2 * 9, 8 = 41, 16
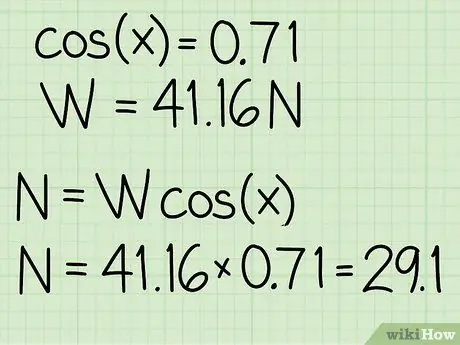
Étape 4. Multipliez les deux valeurs
Pour trouver la force normale, vous devez multiplier le poids de l'objet par le cosinus de l'angle d'inclinaison.
Exemple: N = m * g * cos(x) = 41, 16 * 0, 71 = 29, 1
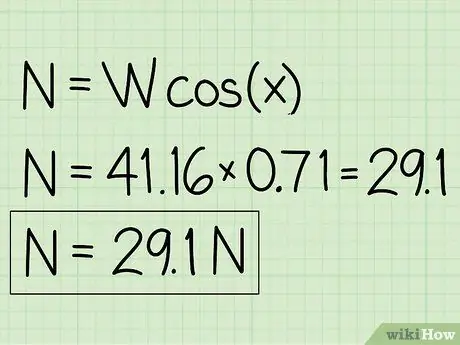
Étape 5. Écrivez vos réponses
L'étape précédente résoudra le problème et fournira votre réponse.
- Notez que lorsqu'un objet est au repos sur une pente, la force normale sera inférieure au poids de l'objet.
- Exemple: La force normale est de 29,1 N.
Méthode 3 sur 5: Style normal avec style extérieur vers le bas
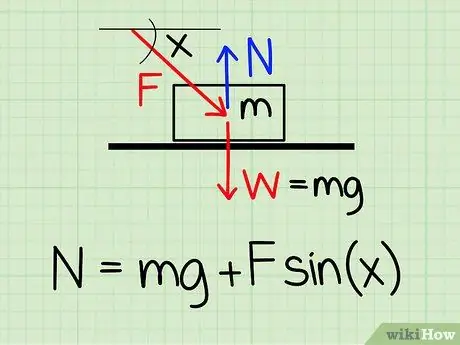
Étape 1. Utilisez la bonne équation
Pour calculer la force normale sur un objet au repos s'il y a une force externe vers le bas sur l'objet, utilisez l'équation: N = m * g + F * sin(x)'
- N symbolise le style normal, m représente la masse de l'objet g représente l'accélération due à la pesanteur, F symbolise le style extérieur, et X représente l'angle entre l'objet et la direction de la force externe.
- Exemple: Trouvez la force normale d'un objet avec une masse de 4,2 kg si l'objet est poussé par une personne à un angle de 30 degrés et une force de 20,9 N.
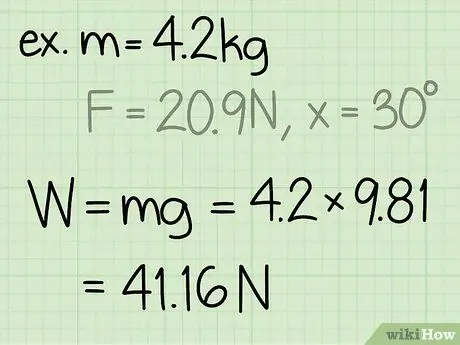
Étape 2. Trouvez le poids de l'objet
Le poids d'un objet est égal à la masse de l'objet multipliée par l'accélération due à la gravité.
- Notez que l'accélération due à la gravité à la surface de la terre est toujours constante: g = 9,8 m/s2
- Exemple: poids = m * g = 4, 2 * 9, 8 = 41, 16
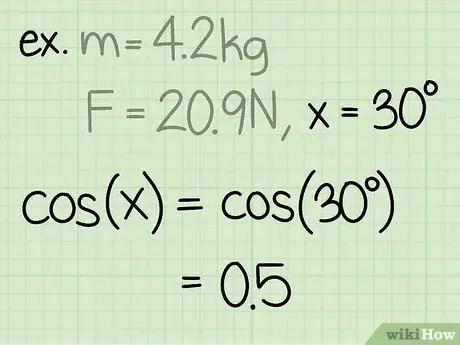
Étape 3. Trouvez le sinus de l'angle
Le sinus d'un angle se calcule en divisant le côté du triangle opposé à l'angle par l'hypoténuse de l'angle.
Exemple: sin(30) = 0.5

Étape 4. Multipliez le sinus par la force externe
La force externe, dans cet exemple, fait référence à la force descendante frappant l'objet.
Exemple: 0, 5 * 20, 9 = 10, 45
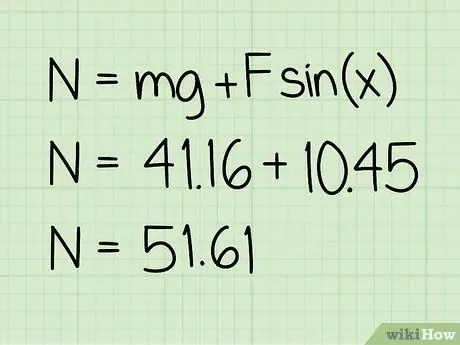
Étape 5. Ajoutez cette valeur au poids
Cette somme donnera l'amplitude de la force normale agissant.
Exemple: 10, 45 + 41, 16 = 51, 61
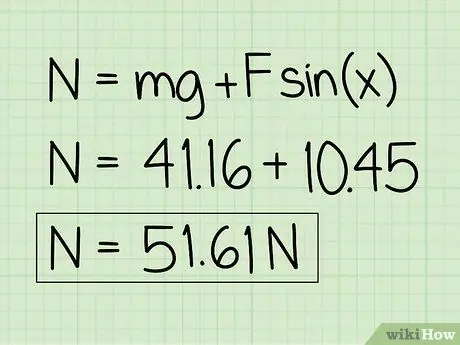
Étape 6. Écrivez vos réponses
Notez que pour un objet au repos qui est affecté par une force externe vers le bas, la force normale sera supérieure au poids de l'objet.
Exemple: La force normale est de 51,61 N
Méthode 4 sur 5: Style normal avec style extérieur vers le haut
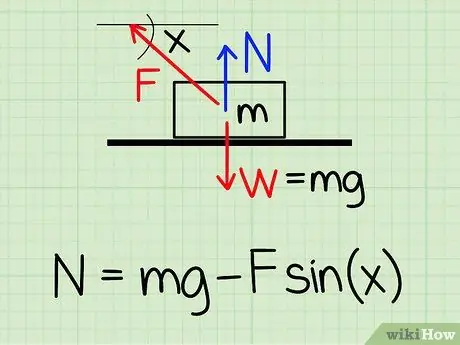
Étape 1. Utilisez la bonne équation
Pour calculer la force normale sur un objet au repos s'il y a une force externe vers le haut sur l'objet, utilisez l'équation: N = m * g - F * sin(x)'
- N symbolise le style normal, m représente la masse de l'objet g représente l'accélération due à la pesanteur, F symbolise le style extérieur, et X représente l'angle entre l'objet et la direction de la force externe.
- Exemple: Trouvez la force normale d'un bloc d'une masse de 4,2 kg, si quelqu'un tire le bloc vers le haut à un angle de 50 degrés et une force de 20,9 N.

Étape 2. Trouvez le poids de l'objet
Le poids d'un objet est égal à la masse de l'objet multipliée par l'accélération due à la gravité.
- Notez que l'accélération due à la gravité à la surface de la terre est toujours constante: g = 9,8 m/s2
- Exemple: poids = m * g = 4, 2 * 9, 8 = 41, 16
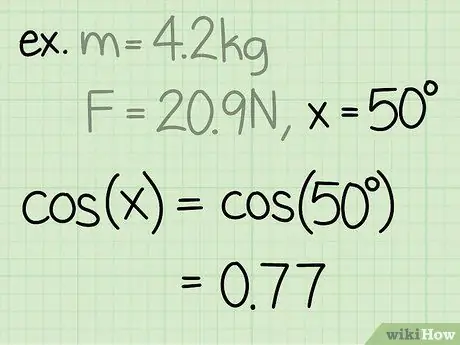
Étape 3. Trouvez le sinus de l'angle
Le sinus d'un angle se calcule en divisant le côté du triangle opposé à l'angle par l'hypoténuse de l'angle.
Exemple: sin(50) = 0, 77

Étape 4. Multipliez le sinus par la force externe
La force externe fait référence à la force ascendante frappant l'objet, dans ce cas.
Exemple: 0,77 * 20, 9 = 16, 01
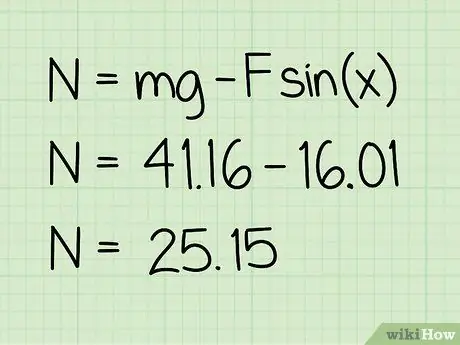
Étape 5. Soustrayez cette valeur du poids
La soustraction que vous faites vous donnera l'amplitude de la force normale agissant sur elle.
Exemple: 41, 16 - 16, 01 = 25, 15
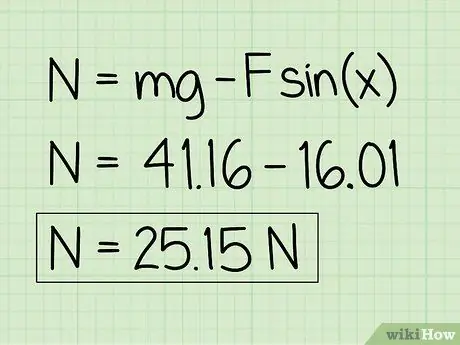
Étape 6. Écrivez vos réponses
Notez qu'un objet au repos est affecté par une force externe ascendante, la force normale sera inférieure au poids de l'objet.
Exemple: La force normale est de 25, 15 N
Méthode 5 sur 5: Force normale et friction

Étape 1. Connaître l'équation de base du frottement cinétique
Le frottement cinétique, ou frottement d'un objet en mouvement, est égal au coefficient de frottement multiplié par la force normale d'un objet. Sous forme d'équation: f = * N
- Dans cette équation, F symboliser la friction, ️ représente le coefficient de frottement, et N représente la force normale de l'objet.
- Le "coefficient de friction" est le rapport de la force de friction à la force normale, qui comprime deux surfaces opposées.
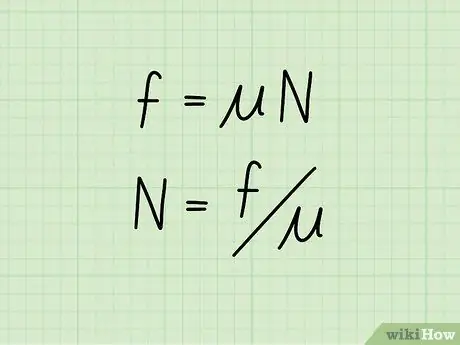
Étape 2. Configurez l'équation pour isoler la force normale
Si vous connaissez la valeur du frottement cinétique d'un objet, ainsi que son coefficient de frottement, vous pouvez calculer la force normale en utilisant la formule: N = f /
- Les deux côtés de l'équation originale sont divisés par ️, isolant ainsi la force normale d'un côté tout en calculant le coefficient de frottement et le frottement cinétique de l'autre.
- Exemple: Trouvez la force normale d'un bloc si le coefficient de frottement est de 0,4 et l'amplitude du frottement cinétique est de 40 N.
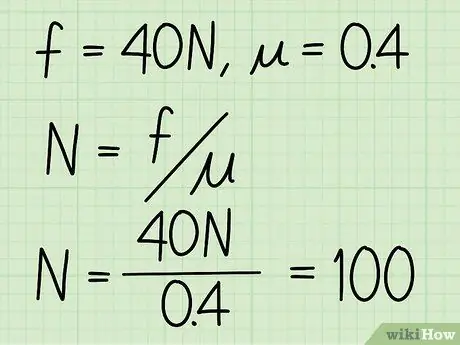
Étape 3. Divisez le frottement cinétique par le coefficient de frottement
Fondamentalement, c'est tout ce que vous devez faire pour trouver l'amplitude de la force normale.
Exemple: N = f / = 40 / 0, 4 = 100
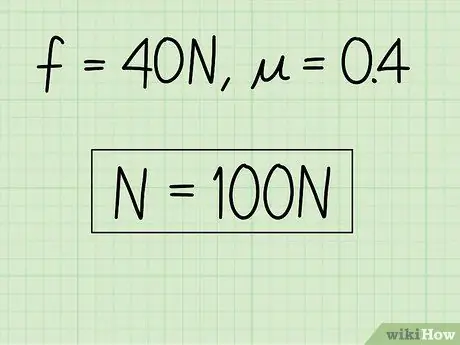
Étape 4. Notez vos réponses
Si vous le souhaitez, vous pouvez vérifier votre réponse en la rebranchant dans l'équation d'origine pour le frottement cinétique. Si vous ne le voulez pas, vous avez résolu le problème.






