La réciproque ou la réciproque est très utile dans toutes sortes d'équations algébriques. Par exemple, lorsque vous divisez une fraction par une autre, vous multipliez la première fraction par l'inverse de la seconde. Vous devez également utiliser l'inverse lorsque vous recherchez l'équation d'une ligne.
Étape
Méthode 1 sur 3: Trouver l'inverse d'une fraction ou d'un entier
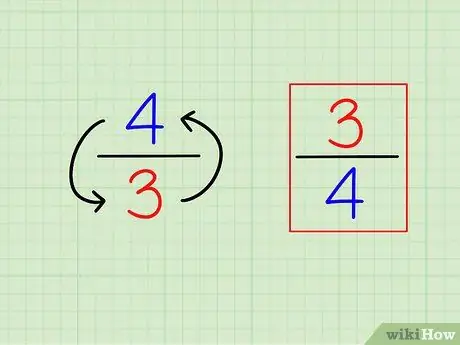
Étape 1. Trouvez l'inverse de la fraction en l'inversant
La définition de « réciproque » ou l'inverse est très simple. Pour trouver l'inverse d'un nombre entier, calculez simplement "1 (ce nombre)". Pour les fractions, l'inverse est une fraction différente, c'est-à-dire que les nombres sont « inversés » (inverse).
- Par exemple, le contraire de 3/4 est 4/3.
- Tout nombre multiplié par sa réciproque renvoie 1.
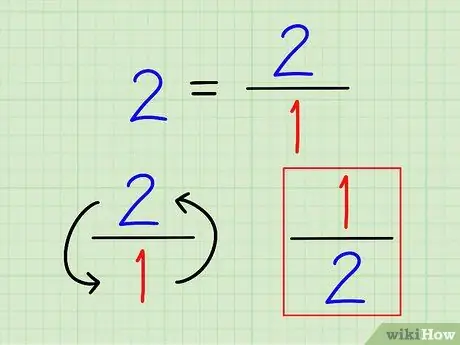
Étape 2. Écrivez l'inverse du nombre entier sous forme de fraction
Encore une fois, l'inverse d'un nombre est toujours 1 (ce nombre). Pour les nombres entiers, écris-les sous forme de fractions. Il ne sert à rien de calculer ce nombre à une décimale.
Par exemple, l'inverse de 2 est 1 2 = 1/2.
Méthode 2 sur 3: Trouver l'inverse d'une fraction mixte
Étape 1. Identifiez les nombres mixtes
Les fractions mixtes sont constituées de nombres entiers et de fractions, tels que 24/5. Il y a deux étapes pour trouver l'inverse d'un nombre mixte comme décrit ci-dessous.
Étape 2. Convertissez les nombres fractionnaires en fractions impropres
N'oubliez pas que 1 peut toujours être écrit sous la forme (nombre)/(même nombre) et que les fractions avec le même dénominateur (nombre du bas) peuvent être additionnées. Voici un exemple utilisant 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
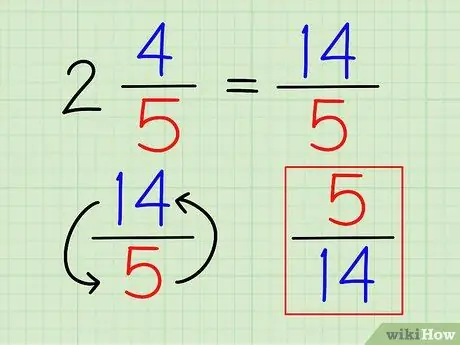
Étape 3. Retournez la fraction
Une fois que le nombre est écrit complètement sous forme de fraction, vous pouvez trouver sa réciproque comme vous le feriez pour n'importe quelle autre fraction, en inversant la fraction.
Dans l'exemple ci-dessus, la réciproque de 14/5 est 5/14.
Méthode 3 sur 3: Trouver l'opposé d'un nombre décimal
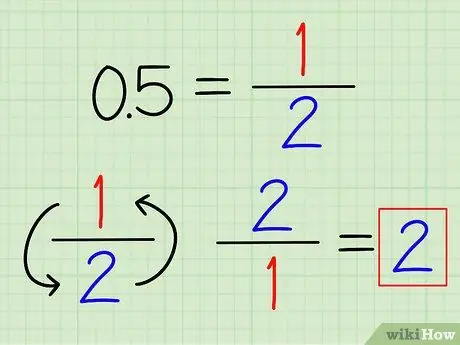
Étape 1. Convertissez les nombres décimaux en fractions si possible
Vous pouvez reconnaître certains nombres décimaux fréquemment utilisés, qui peuvent être facilement convertis en fractions. Par exemple, 0,5 = 1/2 et 0,25 = 1/4. Une fois que la décimale a été convertie en fraction, retournez simplement la fraction pour trouver sa réciproque.
Par exemple, l'inverse de 0,5 est 2/1 = 2.
Étape 2. Écrivez un problème de division
Si vous ne pouvez pas le convertir en fraction, calculez l'inverse du nombre sous la forme d'un problème de division: 1 (décimal). Vous pouvez utiliser une calculatrice pour le résoudre ou passer à l'étape suivante pour le résoudre manuellement.
Par exemple, vous pouvez trouver l'inverse de 0,4 en calculant 1 0,4
Étape 3. Modifiez le problème de division pour utiliser des nombres entiers
La première étape pour diviser des nombres décimaux consiste à déplacer la virgule jusqu'à ce que tous les nombres soient des nombres entiers. Tant que vous déplacez la virgule décimale des deux nombres du même nombre de pas, vous obtiendrez la bonne réponse.
Par exemple, vous pouvez utiliser 1 0, 4 et le réécrire sous la forme 10 4. Dans ce cas, vous déplacez toutes les décimales d'un pas vers la droite, de la même manière que vous multipliez chaque nombre par dix
Étape 4. Résolvez le problème en utilisant la division longue
Utilisez la méthode de la division longue pour calculer la réciproque. Si vous comptez 10 4, vous obtiendrez la réponse 2, 5 qui est l'inverse de 0, 4.
Des astuces
- L'inverse négatif d'un nombre est le même que l'inverse régulier, en ce sens qu'il est multiplié par moins un. Par exemple, l'inverse négatif de 3/4 est -4/3.
- L'inverse ou l'inverse est souvent appelé "l'inverse de la multiplication".
- Le chiffre 1 est l'opposé de lui-même car 1 1 = 1.
- Le nombre 0 n'a pas de réciproque car 0 n'est pas défini.
