Vous ne savez pas dessiner des équations linéaires sans utiliser de calculatrice ? Heureusement, tracer des équations linéaires est assez facile si vous savez comment. Tout ce que vous avez à faire est de comprendre quelques éléments de votre équation et vous serez capable de le faire. Commençons.
Étape
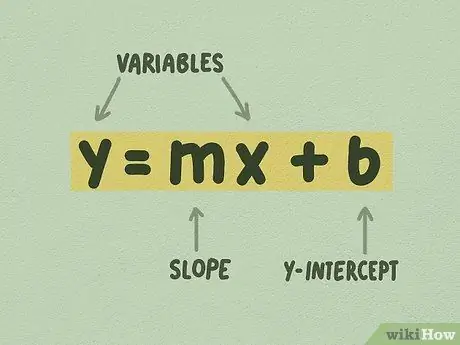
Étape 1. Assurez-vous que l'équation linéaire a la forme y = mx + b
Cette forme s'appelle la forme d'ordonnée à l'origine et est probablement la forme la plus simple à utiliser pour représenter graphiquement des équations linéaires. La valeur dans l'équation ne doit pas nécessairement être un nombre entier. Souvent, vous verrez une équation qui ressemble à ceci: y = 1/4x + 5, où 1/4 est m et 5 est b.
- m est appelé la « pente », ou parfois le « gradient ». La pente est définie comme l'augmentation sur le côté, ou le changement de y divisé par le changement de x.
- b est défini comme « ordonnée à l'origine ». L'ordonnée à l'origine est le point où la ligne coupe l'axe Y.
- x et y sont des variables. Vous pouvez résoudre une valeur x spécifique, par exemple, si vous avez un point y et connaissez les valeurs de m et b. Cependant, x, n'a jamais qu'une seule valeur: sa valeur change au fur et à mesure que la ligne monte ou descend.
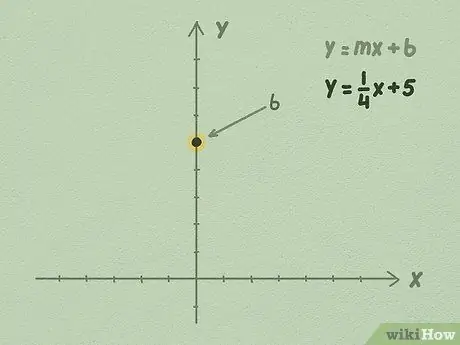
Étape 2. Dessinez le nombre b sur l'axe Y
Votre valeur b sera toujours un nombre rationnel. Quel que soit le nombre b, trouvez sa valeur sur l'axe Y et placez le nombre à un point sur l'axe vertical.
Par exemple, utilisons l'équation y = 1/4x + 5. Puisque le dernier nombre est b, nous savons que b est égal à 5. Remontez de 5 points sur l'axe Y et marquez les points. C'est là que votre ligne droite croisera l'axe Y
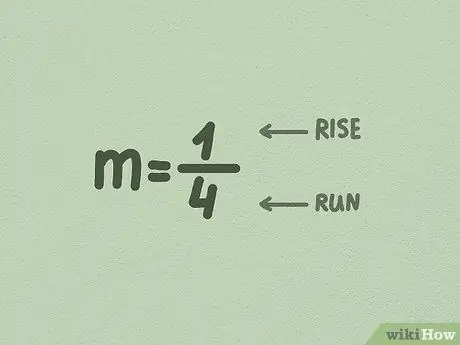
Étape 3. Convertissez m en fraction
Souvent, le nombre devant x est déjà une fraction, vous n'avez donc pas besoin de le changer. Mais sinon, changez-le simplement en plaçant la valeur de m sous le nombre 1.
- Le premier nombre (le numérateur) est l'incrément en ordre croissant divisé par le côté. Ce nombre indique jusqu'où la ligne monte, ou verticalement.
- Le deuxième nombre (le dénominateur) est le côté ascendant divisé par le côté. Ce nombre indique dans quelle mesure la ligne se déplace latéralement ou horizontalement.
- Par exemple:
- La pente de 4/1 se déplace de 4 points vers le haut pour chaque 1 point sur le côté.
- La pente de -2/1 se déplace de 2 points vers le bas pour chaque 1 point sur le côté.
- Une pente de 1/5 déplace 1 point vers le haut tous les 5 points sur le côté.
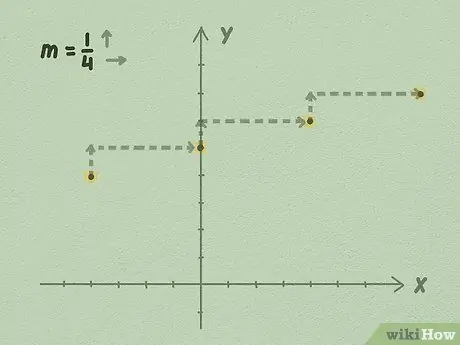
Étape 4. Commencez à prolonger la ligne à partir de b en utilisant la pente, ou vers le haut divisé par le côté
Commencez par votre valeur b: nous savons que l'équation dépasse ce point. Prolongez la ligne en prenant votre pente et en utilisant sa valeur pour obtenir les points de l'équation.
- Par exemple, en utilisant l'illustration ci-dessus, vous pouvez voir que pour chaque point vers le haut, la ligne se déplace de 4 points vers la droite. Cela se produit parce que la pente de la ligne est 1/4. Vous prolongez la ligne indéfiniment des deux côtés, en continuant à utiliser divisé par le côté pour tracer la ligne.
- La pente est positive en montant, tandis que la pente est négative en descendant. Une pente de -1/4 par exemple, descendra de 1 point tous les 4 points latéralement.
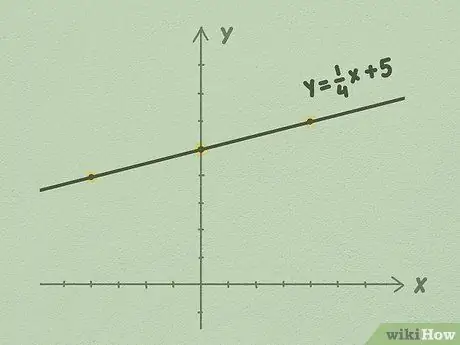
Étape 5. Continuez à étendre la ligne, à l'aide d'une règle et en vous assurant d'utiliser la pente, m, comme guide
Prolongez la ligne indéfiniment et vous avez terminé de représenter graphiquement votre équation linéaire. Assez facile, non?
