- Auteur Jason Gerald [email protected].
- Public 2023-12-16 11:11.
- Dernière modifié 2025-01-23 12:18.
Compter des fractions est l'une des compétences mathématiques les plus utiles à développer. Avant de faire des calculs fractionnaires, apprenez à identifier les parties et les types de fractions. Après cela, vous pouvez les ajouter ou les soustraire. Pour des calculs plus complexes, apprenez à multiplier et à diviser des fractions. Habituellement, vous devrez également simplifier ou réduire les fractions.
Étape
Méthode 1 sur 4: Reconnaître les fractions

Étape 1. Trouvez la fraction
Les fractions sont écrites sous la forme d'un nombre au-dessus de la ligne de séparation et d'un autre nombre en dessous de la ligne.
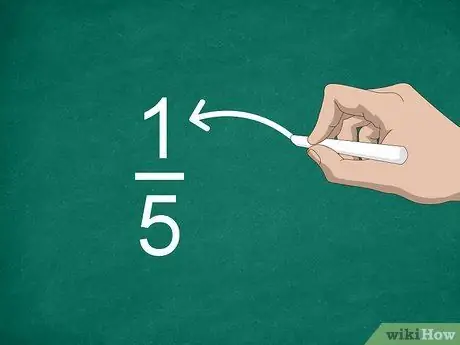
Étape 2. Identifiez le numérateur
Le nombre au-dessus de la ligne s'appelle le numérateur et indique combien de parties il y a dans la fraction.
Par exemple, dans la fraction 1/5, « 1 » est le numérateur
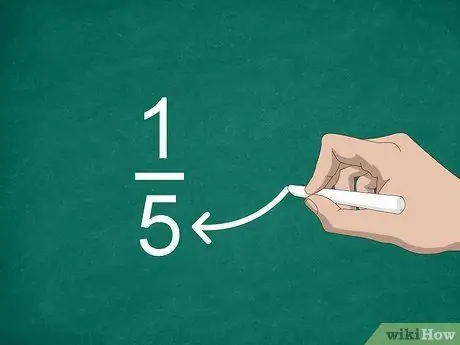
Étape 3. Trouvez le dénominateur
Le nombre placé sous la ligne est appelé le dénominateur. Cette valeur indique le nombre de parties qui "construisent" un entier.
Par exemple, dans la fraction 1/5, "5" est le dénominateur donc il y a cinq parties à la fraction

Étape 4. Déterminez si les fractions sont des fractions raisonnables ou des fractions impropres
Si le numérateur est plus petit que le dénominateur, la fraction est une fraction naturelle. Dans les fractions impropres, le numérateur est supérieur au dénominateur.
- Par exemple, 3/4 est une fraction raisonnable et 5/3 est une fraction impropre.
- Si vous avez un nombre entier qui inclut une fraction, le nombre est appelé nombre mixte. Par exemple, 1 1/2 est un nombre mixte.
Méthode 2 sur 4: Ajouter ou soustraire des fractions

Étape 1. Identifiez les fractions ayant le même dénominateur
Si vous devez additionner ou soustraire des fractions, chaque fraction doit avoir le même dénominateur avant d'effectuer le calcul. Observez le dénominateur de chaque fraction pour vous assurer qu'elles sont toutes égales (similaires).
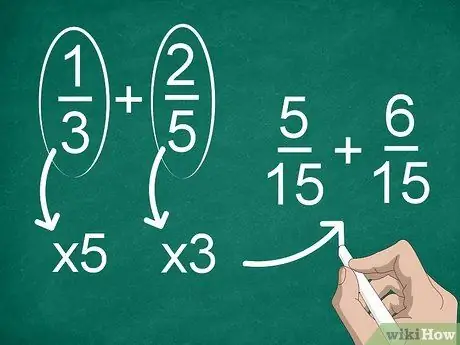
Étape 2. Trouvez un dénominateur commun si chaque fraction a un dénominateur différent
Si les dénominateurs ne sont pas les mêmes, vous devrez changer les fractions pour avoir le même dénominateur. Pour trouver un dénominateur commun, multipliez chaque fraction par le dénominateur de l'autre.
Par exemple, pour trouver un dénominateur commun en 1/3 + 2/5, multipliez « 1 » et « 3 » par « 5 », puis multipliez « 2 » et « 5 » par « 3 ». Maintenant, vous avez l'ajout de 5/15 + 6/15. Après cela, vous pouvez calculer les fractions
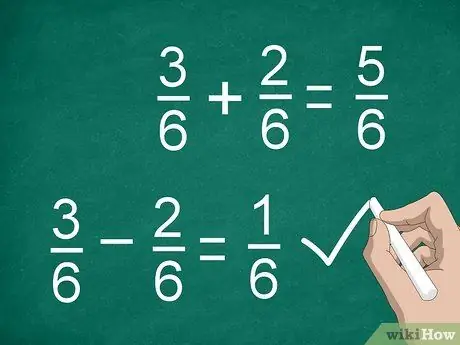
Étape 3. Ajoutez ou soustrayez les numérateurs pour calculer les fractions
Une fois que vous avez trouvé un dénominateur commun et multiplié les numérateurs (si nécessaire), vous êtes prêt à additionner ou soustraire. Additionnez ou soustrayez les numérateurs et placez le résultat au-dessus de la ligne de séparation. Écris le dénominateur commun sous la ligne.
- Par exemple, 3/6 - 2/6 = 1/6.
- Ne pas ajouter ou soustraire les dénominateurs.
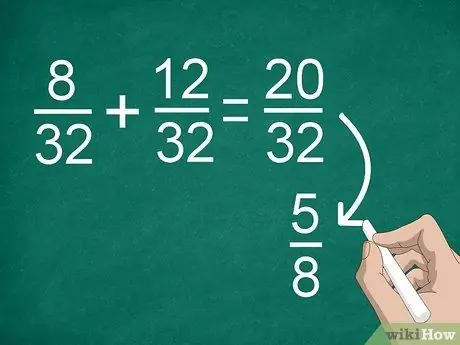
Étape 4. Simplifiez les résultats si nécessaire
Si vous aviez auparavant besoin de trouver un dénominateur commun, vous pourriez obtenir une fraction importante que vous pouvez simplifier. Par exemple, si vous ajoutez 8/32 +12/32, vous obtiendrez « 20/32 » comme résultat. Cette fraction peut être simplifiée en « 5/8 ».
Méthode 3 sur 4: Multiplier et simplifier des fractions
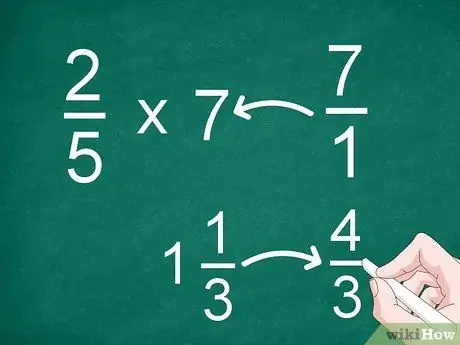
Étape 1. Convertissez des fractions mixtes ou des nombres entiers en fractions impropres
Pour faciliter la multiplication, vous devez convertir chaque nombre en une fraction raisonnable ou impropre. Si vous avez des nombres entiers ou des nombres fractionnaires à multiplier, convertissez-les d'abord en une fraction commune (naturelle ou impropre).
- Par exemple, pour multiplier 2/5 par 7, convertissez "7" en fraction. Après cela, vous pouvez multiplier 2/5 par 7/1.
- Si vous avez un nombre mixte comme 1 1/3, convertissez-le en une fraction impropre (« 4/3 ») avant de multiplier.
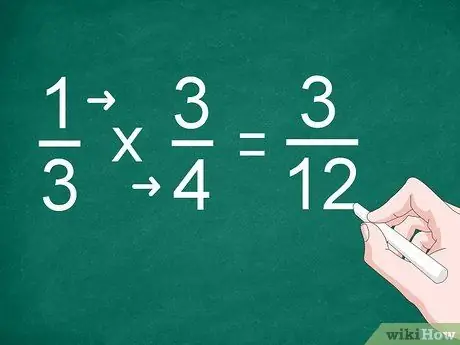
Étape 2. Multipliez chaque numérateur et dénominateur
Au lieu de faire l'addition, multipliez le numérateur et écrivez le résultat au-dessus de la ligne de séparation. Vous devez également multiplier les dénominateurs et écrire le résultat sous la ligne.
Par exemple, pour multiplier 1/3 par 3/4, multipliez « 1 » par « 3 » pour obtenir le numérateur. Multipliez « 3 » par « 4 » pour obtenir le dénominateur. La réponse à la multiplication est "3/12"

Étape 3. Simplifiez les résultats
Habituellement, vous devrez réduire le résultat à une forme plus simple, surtout si vous avez initialement des fractions non naturelles. Trouvez le plus grand facteur commun et utilisez ce facteur pour simplifier le numérateur et le dénominateur.
Par exemple, pour la fraction 3/12, le plus grand facteur commun entre « 3 » et « 12 » est « 3 ». Divisez chaque élément de la fraction par « 3 » jusqu'à ce que vous obteniez la fraction « 1/4 »
Méthode 4 sur 4: Diviser les fractions
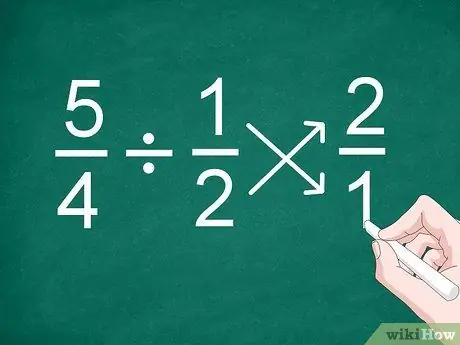
Étape 1. Inversez la position de la deuxième fraction
Le moyen le plus simple de diviser des fractions, même des fractions avec des dénominateurs différents, est d'inverser la position de la deuxième fraction avant de calculer le résultat.
Par exemple, pour le problème 5/4 1/2, inversez la position de la fraction « 1/2 » pour devenir « 2/1 »
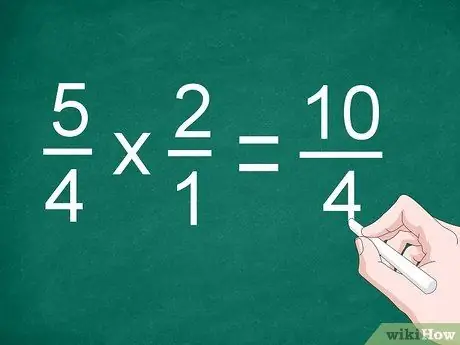
Étape 2. Multipliez le numérateur et le dénominateur
Multipliez directement les fractions pour multiplier les numérateurs. Écrivez le résultat au-dessus de la ligne de séparation, puis multipliez le dénominateur. Enregistrez le produit des dénominateurs sous la ligne.
Pour l'exemple précédent, multipliez 5/4 par 2/1 pour obtenir « 10/4 »
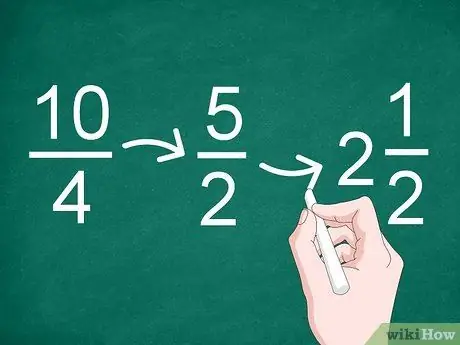
Étape 3. Simplifiez les résultats si nécessaire
Si le résultat de la division est une fraction impropre ou peut être réduite, simplifiez la fraction. Utilisez le plus grand facteur commun pour réduire la fraction.
- Par exemple, le plus grand facteur commun à la fraction 10/4 est « 2 », donc le résultat de la simplification devient « 5/2 » (10 divisé par 2 et 4 divisé par 2).
- Étant donné que le résultat de la simplification est une fraction impropre, vous pouvez le convertir en un entier et une fraction (un nombre mixte). Par conséquent, 5/2 peut être changé en « 2 ».
Des astuces
- Si vous travaillez avec des fractions complexes, vous devrez suivre quelques étapes supplémentaires pour simplifier la fraction. Cependant, cette simplification elle-même est une partie obligatoire du processus de calcul.
- Écrivez toujours les fractions soigneusement pour réduire le risque d'erreurs de calcul.






