- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:11.
- Dernière modifié 2025-01-23 12:18.
Si vous comprenez déjà, convertir des fractions ordinaires en nombres décimaux n'est pas difficile. Pour convertir des fractions courantes en nombres décimaux, vous pouvez utiliser une division longue, une multiplication ou même une calculatrice si vous ne souhaitez pas calculer à la main. Une fois que vous aurez maîtrisé la méthode, vous pourrez facilement convertir des fractions en décimales.
Étape
Méthode 1 sur 4: Avec Division Longue
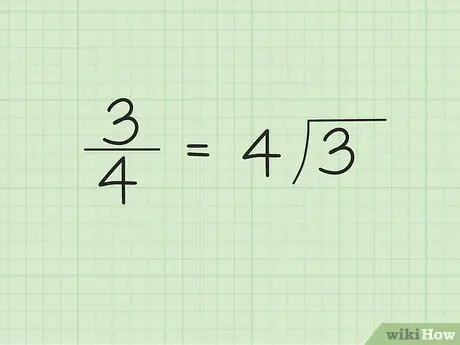
Étape 1. Écrivez le dénominateur à l'extérieur/à gauche du symbole diviseur et le numérateur à l'intérieur/à droite du symbole diviseur
Par exemple, disons que nous voulons convertir 3/4 en nombre décimal. Écrivez « 4 » à l'extérieur/à gauche du symbole du diviseur et « 3 » à l'intérieur/à droite du symbole du diviseur. « 4 » est le nombre qui divise et « 3 » est le nombre qui est divisé.

Étape 2. Écrivez « 0 », puis un point décimal (une virgule), au-dessus du symbole diviseur
Comme c'est une fraction qui compte, le résultat doit être inférieur à un, donc cette étape est très importante. Après cela, écrivez le signe décimal, puis « 0 », après le chiffre « 3 » à l'intérieur/à droite du symbole diviseur. Même si « 3 » est égal à « 3, 0 », le zéro permet de diviser « 3, 0 » par « 4 ».

Étape 3. Calculez la réponse en utilisant la division longue
Avec une division longue, pour l'instant, le signe décimal peut être ignoré, vous n'avez donc qu'à calculer 30 divisé par 4. Voici comment:
- Tout d'abord, divisez 3, 0, qui compte pour 30, par 4. Le 4 à 30 le plus proche est 4 x 7 = 28, laissant 2. Donc, écrivez « 7 » après « 0 », au-dessus du diviseur et « 28 » sous « 3, 0" in/côté droit du symbole diviseur. Moins de 28 ans, écrivez "2", le reste de 30 moins 28.
- Ensuite, écrivez « 0 » après « 3, 0 » pour qu'il devienne « 3, 00 », qui peut être considéré comme « 300 », à l'intérieur/à droite du symbole diviseur. Ainsi, 0 peut être abaissé à droite de "2" pour que "20" soit divisible par "4".
- « 20 » divisé par « 4 » équivaut à « 5 ». Donc, écrivez « 5 » après « 0,7 » au-dessus du symbole diviseur pour qu’il devienne « 0,75 ».

Étape 4. Écrivez la réponse finale
Ainsi, « 3 » divisé par « 4 » équivaut à « 0,75 ». Écrivez la réponse. Fini.
Méthode 2 sur 4: Fractions générant des nombres décimaux répétés
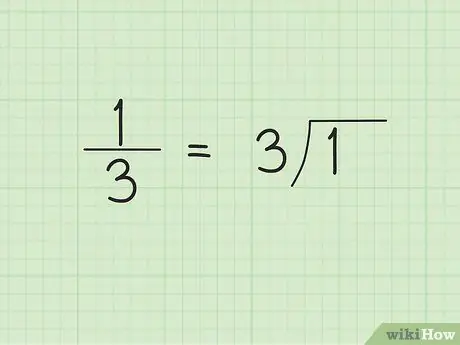
Étape 1. Faites une division longue
Lorsque vous commencez une division à longs chiffres, vous ne pourrez peut-être pas prédire que le résultat sera un nombre décimal répétitif. Par exemple, disons que nous voulons convertir la fraction commune 1/3 en forme décimale. Écrivez 3, ou le dénominateur, du côté extérieur/gauche du symbole diviseur et 1 du côté intérieur/droit du symbole diviseur.

Étape 2. Écrivez un 0, puis un signe décimal, au-dessus du symbole diviseur
Comme le résultat doit être inférieur à 1, cette étape prépare la réponse à être écrite sous forme décimale. Le signe décimal doit également être écrit à droite du chiffre « 1 » qui se trouve dans/à droite du symbole diviseur.
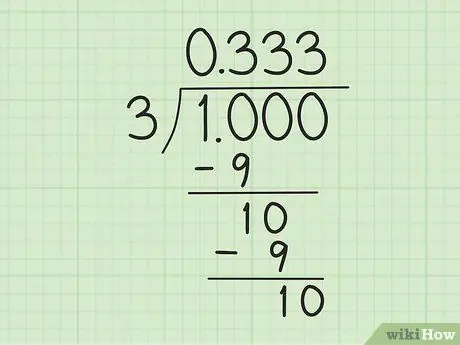
Étape 3. Commencez à calculer la division longue
Commencez par transformer « 1 » en « 1, 0 », qui compte pour « 10 », afin qu'il soit divisible par « 3 ». Ensuite, effectuez les étapes suivantes:
- Divisez 10 par 3. Utilisez 3 x 3 = 9 pour obtenir un reste de 1. Écrivez donc 3 à droite du « 0 » au-dessus du symbole diviseur et soustrayez 10 par 9 pour obtenir un reste de 1.
- Écrivez un "0" à droite du nombre "1" (le reste de 10 moins 9 à l'étape précédente) ci-dessous pour obtenir un autre "10". Lorsque vous divisez à nouveau « 10 » par « 3 », le même processus est répété: écrivez « 3 » à droite du premier « 3 » au-dessus du symbole diviseur et soustrayez le nouveau « 10 » par « 9 ».
- Continuez jusqu'à ce qu'un motif se forme. Tu sais que quelque chose est bizarre ? Cette division peut durer éternellement. 10 est toujours divisible par 3: il y aura toujours un "1" en bas et un nouveau "3" après la virgule au-dessus du symbole diviseur.
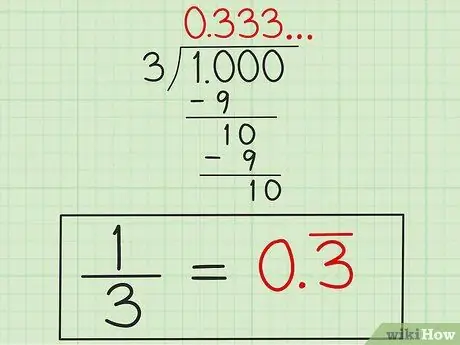
Étape 4. Écrivez la réponse
Après avoir su que « 3 » se répétera, écrivez la réponse sous la forme « 0, 3 » avec une ligne au-dessus du nombre « 3 » (ou « 0, 33 » avec une ligne au-dessus des deux nombres « 3 » pour indiquer que le numéro "3" il ne cesse de répéter. Cette réponse est sous la forme décimale 1/3 car 1 divisé par 3 ne se terminera pas tout seul.
Il existe de nombreuses fractions qui produisent des nombres décimaux répétés, comme 2/9 (« 0, 2 » avec « 2 » répété), 5/6 (« 0, 83 » avec « 3 » répété) ou 7/9 (« 0, 7" avec "7" ne cesse de se répéter). Ce modèle se produit toujours lorsque le dénominateur est un multiple de 3 et que le numérateur ne peut pas être divisible par le dénominateur
Méthode 3 sur 4: Par multiplication

Étape 1. Trouvez le nombre qui peut être multiplié par le dénominateur de la fraction pour produire 10, 100, 1 000 ou tout autre nombre en base 10
Cela peut être un moyen facile de convertir des fractions en nombres décimaux sans utiliser de longues divisions ou une calculatrice. Tout d'abord, trouvez simplement un nombre qui peut être multiplié par le dénominateur de la fraction pour obtenir 10, 100, 1 000, etc. Pour ce faire, divisez d'abord 10, puis 100, puis 1 000, et ainsi de suite par le dénominateur jusqu'à ce que vous obteniez un nombre entier. Exemple:
- 3/5. 10/5 = 2,2 est un entier. 2 peut être multiplié par 5 pour faire 10. Donc, 2 peut être utilisé.
- 3/4. 10/4 = 2, 5. 2, 5 n'est pas un nombre entier. 100/4 = 25. 25 est un nombre entier. 25 peut être multiplié par 4 pour faire 100. Donc 25 peut être utilisé.
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1 000/16 = 62, 5, 10 000/16 = 625. 625 est le premier entier obtenu. 625 peut être multiplié par 16 pour obtenir 10 000. Ainsi, 625 peut être utilisé.
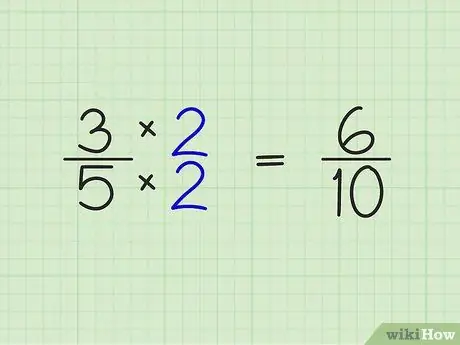
Étape 2. Multipliez le numérateur et le dénominateur de la fraction par le nombre entier obtenu à l'étape précédente
Cette étape est assez facile. Il suffit de multiplier les nombres au-dessus et au-dessous de la fraction par le nombre entier que vous avez obtenu à l'étape précédente. Exemple:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3,125/10000

Étape 3. Écrivez la réponse finale
La réponse est que le numérateur est marqué d'une décimale en fonction du nombre de 0 dans le dénominateur. Comptez simplement le nombre de 0 dans le dénominateur. S'il n'y a que 1 0 au dénominateur, déplacez la virgule vers la gauche d'un chiffre, et ainsi de suite. Exemple:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Méthode 4 sur 4: Avec Calculatrice

Étape 1. Divisez le numérateur par le dénominateur
Cette méthode est très simple. Utilisez simplement une calculatrice pour diviser le numérateur, le nombre en haut de la fraction, par le dénominateur, le nombre en bas de la fraction. Par exemple, supposons que vous vouliez convertir 3/4 en nombre décimal. Appuyez simplement sur "3", puis le symbole de division ("÷'"), puis "4", et enfin le symbole égal ("=").

Étape 2. Notez les réponses que vous obtenez
La réponse est 0,75. Ainsi, la forme décimale de la fraction commune 3/4 est 0,75.
Des astuces
- Pour vérifier si votre réponse est correcte, multipliez la réponse par le dénominateur de la fraction. Si votre réponse est correcte, le produit de la multiplication est le numérateur de la fraction.
- Certaines fractions peuvent être converties en nombres décimaux en créant des fractions comparables dont les dénominateurs sont en base 10 (10, 100, 1 000, etc.). Ensuite, utilisez des valeurs de position pour écrire la forme décimale correcte.






