- Auteur Jason Gerald [email protected].
- Public 2023-12-16 11:11.
- Dernière modifié 2025-01-23 12:18.
Pour la plupart des gens, les fractions sont les premiers calculs compliqués à rencontrer. Le concept de fractions est assez difficile et vous oblige à apprendre des conditions particulières pour le faire. Parce que les fractions ont des règles spéciales pour l'addition, la soustraction, la multiplication et la division, beaucoup de gens sont confus à ce sujet. Cependant, avec beaucoup de pratique, n'importe qui peut apprendre et effectuer des calculs liés aux fractions.
Étape
Méthode 1 sur 5: Comprendre les fractions
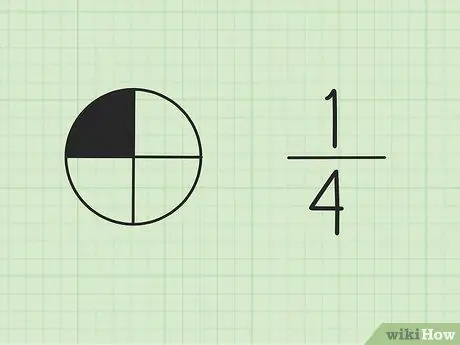
Étape 1. Comprenez que les fractions font partie d'un tout
Le nombre en haut est appelé le numérateur et représente le nombre de parties du total. Le nombre en bas est appelé le dénominateur, qui représente le nombre total de pièces.
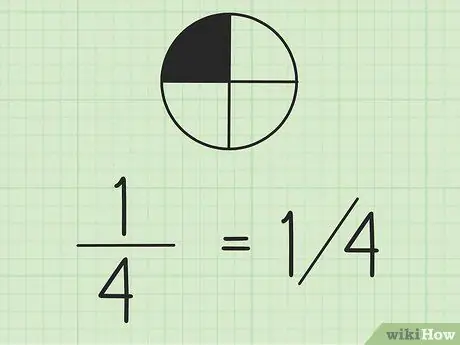
Étape 2. Gardez à l'esprit que vous pouvez écrire des fractions en utilisant des barres obliques
Le nombre de gauche est le numérateur et le nombre de droite est le dénominateur. Si vous travaillez avec des fractions sur la même ligne, c'est une bonne idée d'écrire le numérateur au-dessus du dénominateur.
Par exemple, si vous prenez l'une des quatre tranches de pizza, vous avez une pizza. Si vous avez 7/3 pizzas, cela signifie que vous avez deux pizzas entières plus 1 des 3 tranches de pizza
Méthode 2 sur 5: Différence entre les fractions mixtes et simples

Étape 1. Comprenez que les nombres fractionnaires sont constitués de nombres entiers et de fractions, par exemple 2 1/3 ou 45 1/2
Habituellement, vous devez convertir des nombres mixtes en une forme plus simple pour ajouter, soustraire, multiplier ou diviser.

Étape 2. Modifiez le nombre mixte en multipliant le nombre entier par le dénominateur dans la fraction, puis en l'ajoutant par le numérateur
Écrivez le résultat au numérateur, tandis que le dénominateur ne change pas.
Par exemple, pour convertir 2 1/3 en une fraction simple, multipliez 2 par 3, puis ajoutez 1 et obtenez 7/3

Étape 3. Convertissez des fractions simples en nombres fractionnaires en divisant le numérateur par le dénominateur
Le résultat entier de la division est écrit sous forme d'entier et le reste de la division est écrit sous forme de numérateur de la fraction. Le dénominateur ne change pas.
Par exemple, pour convertir 7/3 en un nombre mixte, divisez 7 par 3 pour obtenir 2 avec un reste de 1. Le nombre mixte est donc 2 1/3. Les fractions simples ne peuvent être converties en nombres fractionnaires que si le numérateur est supérieur au dénominateur
Méthode 3 sur 5: Ajouter et soustraire des fractions
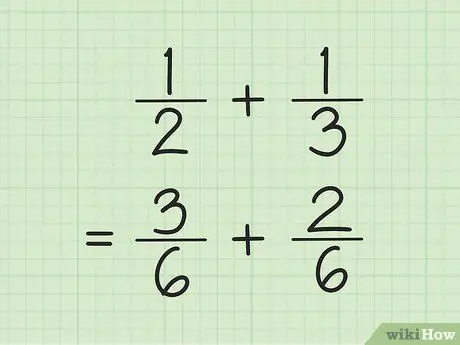
Étape 1. Trouvez un dénominateur commun pour additionner et soustraire des fractions
L'astuce, multiplier les nombres au dénominateur, puis multiplier chaque numérateur par le nombre utilisé pour trouver le dénominateur. Parfois, vous pouvez trouver le LCM (plus petit commun multiple) pour le dénominateur en multipliant les dénominateurs les uns par les autres.
Par exemple, pour additionner et 1/3, trouvez d'abord le LCM (plus petit commun multiple) des deux dénominateurs en les multipliant. Ainsi, vous multipliez 2 et 3 pour obtenir LCM 6. Multipliez 1 par 3 pour obtenir 3 comme nouveau numérateur de la première fraction. Multipliez 1 par 2 pour obtenir 2 comme nouveau numérateur de la deuxième fraction. Vos nouvelles fractions sont 3/6 et 2/6
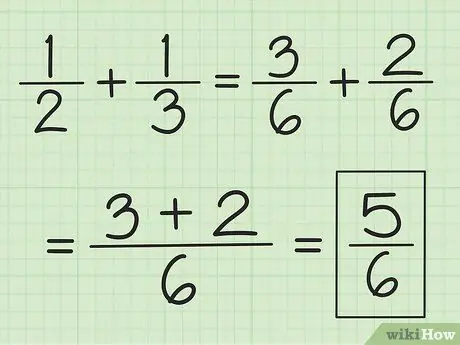
Étape 2. Additionnez les deux numérateurs et ne changez pas le dénominateur
Par exemple, 3/6 plus 2/6 est 5/6, et 2/6 plus 1/6 est 3/6
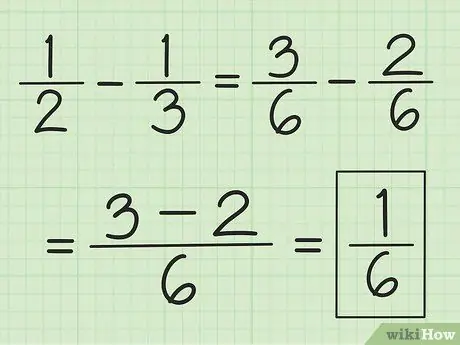
Étape 3. Utilisez une technique similaire pour la soustraction
Trouvez d'abord le LCM des dénominateurs, mais au lieu de les additionner, soustrayez le nombre du premier numérateur par le nombre du second.
Par exemple, pour soustraire 1/3 de 1/2, changez d'abord les fractions en 3/6 et 2/6, puis soustrayez 3 par 2 pour obtenir 1. Cela donne 1/6
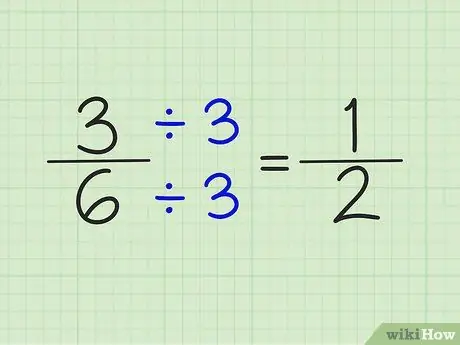
Étape 4. Simplifiez les fractions en divisant le numérateur et le dénominateur par le même nombre
Par exemple, le nombre 5/6 ne peut pas être simplifié. Cependant, 3/6 peut être simplifié en divisant le numérateur et le dénominateur par le nombre 3. Le résultat est une fraction de 1/2

Étape 5. Convertissez la fraction en un nombre mixte si le numérateur est supérieur au dénominateur
Méthode 4 sur 5: Multiplier et diviser des fractions
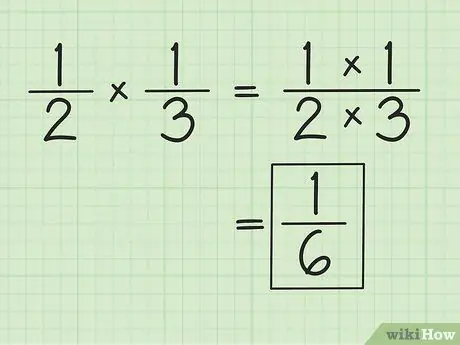
Étape 1. Multipliez le numérateur et le dénominateur séparément pour multiplier les fractions
Par exemple, en multipliant et 1/3, le résultat est 1/6 (1 fois 1 et 2 fois 3). Vous n'avez pas besoin de faire correspondre les dénominateurs lorsque vous multipliez des fractions. Simplifier ou modifier les résultats obtenus, si nécessaire
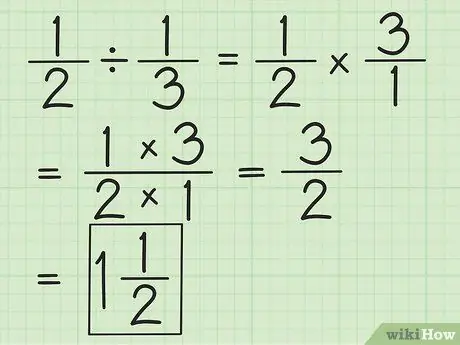
Étape 2. Divisez deux fractions en inversant la deuxième fraction, puis en multipliant les deux
Par exemple, si vous souhaitez diviser 1/2 par 1/3, inversez d'abord la deuxième fraction en 3/1. Multipliez par 3/1 et obtenez 3/2. Simplifiez les fractions ou convertissez-les en nombres mixtes, si possible
Méthode 5 sur 5: Travailler avec des fractions complexes
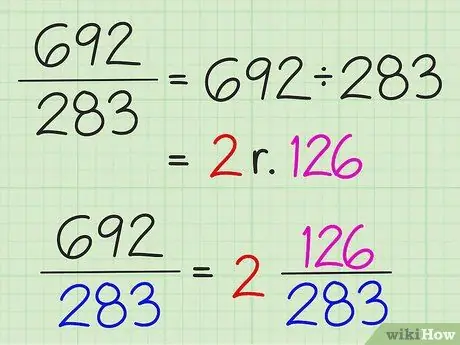
Étape 1. Travaillez toutes les fractions de la même manière, même si le problème semble très compliqué
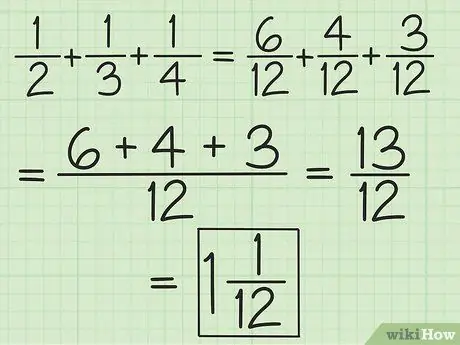
Étape 2. Faites correspondre les dénominateurs de toutes les fractions ou travaillez par paires en commençant de gauche à droite pour additionner et soustraire plus de deux fractions
Par exemple, pour additionner 1/2, 1/3 et 1/4, vous pouvez les changer en 6/12, 4/12 et 3/12 pour obtenir 13/12, ou vous pouvez ajouter 3/6 et 2 /6 donc vous obtenez 5/6, puis ajoutez 5/6 et 1/4 (égalisez les dénominateurs pour que la deuxième fraction devienne 3/12) pour obtenir 13/12 (10/12 plus 3/12). Convertissez-le en un nombre mixte, qui est 1 1/12
Des astuces
- N'oubliez pas que vous avez appris beaucoup de mathématiques. Les mathématiques sont comme une langue que vous pouvez prononcer couramment, et maintenant vous essayez d'apprendre à la lire et à l'écrire.
- N'oubliez pas de toujours simplifier le résultat final de votre calcul, que votre problème soit sous la forme d'une fraction ordinaire, d'un nombre fractionnaire ou d'une fraction complexe.






