3 manières de convertir des unités

2024 Auteur: Jason Gerald | [email protected]. Dernière modifié: 2024-01-19 22:12

Avec différents systèmes de mesure dans le monde, savoir comment convertir des unités peut vous aider. Vous devez comprendre comment calculer des fractions si vous n'utilisez pas le système métrique. Pour chaque système de mesure que vous utilisez, veillez toujours à noter les unités à chaque étape afin de préserver vos résultats.

Étape

Méthode 1 sur 3: Conversion d'unités

Étape 1. Comparez les deux unités

Les deux unités comparées doivent mesurer la même chose. Par exemple, dans la question " convertir 2 pouces en centimètres", les pouces et les centimètres mesurent la longueur. Si vos unités mesurent deux choses différentes (telles que la longueur et le poids), vous ne pouvez pas convertir les deux unités.

• Beaucoup de gens sont souvent confus au sujet de la longueur, de la surface et du volume, mais ce sont trois choses différentes. N'oubliez pas que "carré" ou "²" signifie zone, tandis que "cubique" ou "³" signifie volume.
• Vous pouvez également écrire un exemple comme celui-ci: 2 pouces = ? cm.

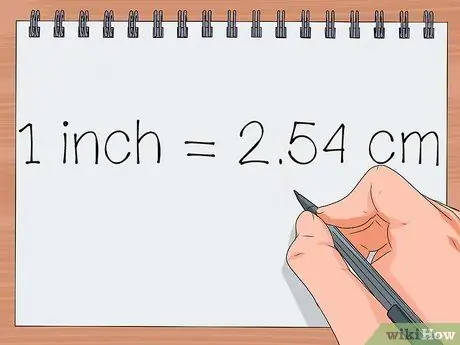
Étape 2. Vérifiez le système de conversion d'unité

Avant de calculer, vous devez connaître la différence entre les unités existantes et les autres. Si vous trouvez une conversion comportant plusieurs décimales, arrondissez au nombre le plus proche. Si vous ne savez pas quel nombre arrondir, arrondissez le deuxième ou le troisième nombre.

Par exemple, si vous devez convertir 2 pouces en centimètres, vous devez savoir que 1 pouce = 2,54 centimètres.

Étape 3. Écrivez la conversion sous forme de fraction

Notez la conversion sous forme de fraction, y compris les unités. Mettez l'unité de départ en bas (le diviseur) et l'unité que vous voulez en haut de la fraction (le numérateur).

Par exemple, écrivez ^{2,54 cm}/_{1 po}. Vous pouvez le lire comme: « 2,54 centimètres par pouce ».

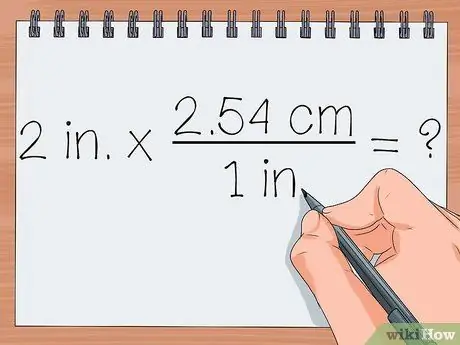
Étape 4. Écrivez un problème de multiplication avec les nombres initiaux et les fractions qui ont été faites

En multipliant ces deux nombres, vous obtiendrez la réponse. Pour ce faire, commencez par écrire un problème de multiplication avec les unités après le nombre.

• 2 pouces X ^{2,54 cm}/_{1 po} = ?

Étape 5. Résolvez le problème de multiplication

Il est important de garder votre compte. Chaque unité du problème doit toujours être présente à chaque étape.

• 2 pouces X ^{2,54 cm}/_{1 po}
• = ^{(2 po x 2,54 cm)}/_{1 po}
• = ^{(5,08 po x cm)}/ _dans.

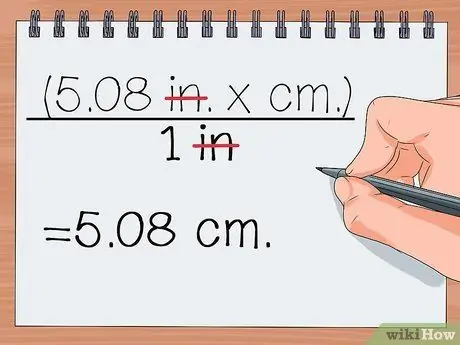
Étape 6. Supprimez les unités qui apparaissent en haut et en bas de la fraction

S'il y a des unités identiques en haut et en bas de la fraction, rayez-les. Les unités restantes doivent être les unités que vous recherchez.

• ^{(5,08 po x cm)}/_dans.

• = 5,08 cm.

  

  Étape 7. Corrigez l'erreur de calcul

  Si aucune unité n'est supprimée, recommencez le calcul à partir de zéro et réessayez. Vous avez peut-être écrit la mauvaise fraction au début du calcul.

  Par exemple, si vous deviez multiplier 2 pouces x (1 pouce / 2,54 cm), votre réponse serait « pouces x pouces / cm », ce qui n'a pas de sens. Si vous inversez la fraction existante, les pouces seront effacés. Par conséquent, recommencez avec 2 pouces x (2,54 cm / 1 pouce)

  Méthode 2 sur 3: Conversion de valeurs avec plusieurs valeurs

  

  Étape 1. Notez le problème que vous souhaitez résoudre

  Assurez-vous que l'unité que vous voulez trouver et notez-la dans le problème de mathématiques. Par exemple:

  • Si un vélo se déplace à 10 milles à l'heure, combien de pieds parcourt-il en une minute ?
  • Écrivez ce problème comme "10 miles / heure = ? pieds / minute" ou " 10 milles/heure = ? pieds / minute".

  

  Étape 2. Trouvez la conversion pour une unité

  N'oubliez pas que vous ne pouvez convertir que 2 unités qui mesurent la même chose. Dans cet exemple, il existe des unités qui mesurent la longueur (miles et pieds) et des unités qui mesurent le temps (heures et minutes). Commencez avec une paire d'unités et recherchez les conversions entre les deux unités.

  • Par exemple, 1 mille = 5 280 pieds.

  

  Étape 3. Multipliez votre nombre par la fraction de conversion

  Comme expliqué dans la section ci-dessus, vous pouvez écrire les conversions sous forme de fractions afin de pouvoir supprimer les mêmes unités. Assurez-vous d'inclure chaque unité dans vos calculs.

  • ^{10 milles} / _h) X ^{5280 pieds} / _milles
  • = ^{52800 milles x pieds} / _{heures x miles}

  

  Étape 4. Supprimez les mêmes unités

  L'une de vos unités sera en haut et en bas de la fraction, vous pouvez donc rayer l'unité. Vous n'avez toujours pas terminé, mais vous vous rapprochez de la réponse.

  • ^{52800 milles x pieds} / _{heures x miles}
  • = ^{52800 pieds} / _heures

  

  Étape 5. Multipliez le problème par la fraction de conversion de la même manière

  Sélectionnez l'unité qui n'a pas été convertie et écrivez la conversion sous forme de fraction. N'oubliez pas de définir la forme de la fraction, afin que vous puissiez rayer les unités lors de la multiplication.

  • Dans cet exemple, vous devez toujours convertir les heures en minutes. 1 heure = 60 minutes.
  • Maintenant, vous avez 52800 pieds/heure. Puisque l'heure est toujours en dessous de la fraction, utilisez une nouvelle fraction avec l'heure au-dessus de la fraction: 1 heure / 60 minutes.
  • ^{52800 pieds} / _heures X ^{1 heure} / _{60 minutes}
  • = ^{880 pieds x heure} / _{heure x minute}

  

  Étape 6. Supprimez les mêmes unités

  Les mêmes unités doivent être barrées, tout comme ce qui a été fait auparavant.

  • ^{880 pieds x heure} / _{heure x minute}
  • = ^{880 pieds} / _min

  

  Étape 7. Répétez les étapes ci-dessus jusqu'à ce que toutes les unités existantes aient été converties

  Si les réponses sont déjà avec les unités que vous voulez, vous avez terminé les calculs. Sinon, essayez de convertir vers une unité différente en utilisant la même méthode.

  • Si vous connaissez cette méthode, vous pouvez écrire l'intégralité de la conversion sur une seule ligne. Par exemple, vous pouvez résoudre des problèmes comme celui-ci:
  • ^{10 milles}/_heures X ^{5280 pieds}/_milles X ^{1 heure}/_{60 minutes}
  • =^{10 milles}/_heures X ^{5280 pieds}/_milles X ^{1 heure}/_{60 minutes}
  • = 10 x 5280 pieds x ¹/_{60 minutes}
  • = 880 pi/min.

  Méthode 3 sur 3: Conversion avec le système métrique

  

  Étape 1. Apprenez à connaître le système métrique

  Le système métrique, également connu sous le nom de système décimal, est un système conçu pour convertir facilement les unités. Pour convertir une unité métrique en une autre, il vous suffit d'utiliser un nombre entier, tel que 10, 100, 1000, etc.

  

  Étape 2. Identifiez le préfixe de l'unité

  Les unités de mesure métriques utilisent un préfixe pour indiquer la taille d'une mesure existante. Bien que les exemples donnés soient en unités de poids, toutes les unités métriques utilisent le même préfixe. Dans l'exemple, le préfixe sera en italique, mais vous pouvez utiliser une conversion avec le préfixe fréquemment utilisé, qui est imprimé épais.

  • kilo grammes = 1000 grammes
  • hectogrammes = 100 grammes
  • déca gramme = 10 gramme
  • grammes = 1 gramme
  • déci gramme = 0,1 gramme (un dixième)
  • pouces gramme = 0,01 gramme (un pour cent)
  • milli gramme = 0,001 gramme (un pour mille)

  

  Étape 3. Utilisez des préfixes dans les conversions

  Si vous connaissez le préfixe d'unité à utiliser, vous n'avez pas besoin de parcourir la liste des préfixes à chaque fois que vous convertissez des unités. Le préfixe d'unité ci-dessus a indiqué la valeur de conversion. Par exemple:

  • Pour convertir des kilomètres en mètres: kilo signifie 1000 puis 1 kilomètre = 1000 mètres.
  • Pour convertir des grammes en milligrammes: milli signifie 0,001 puis 1 milligramme = 0,001 gramme.

  

  Étape 4. Déplacez le point décimal au lieu d'avoir à faire le calcul

  En utilisant les conversions métriques, vous pouvez ignorer toutes les étapes de calcul comme ci-dessus. Multiplier un nombre par 10 revient à déplacer la virgule vers la gauche. Voici un exemple d'utilisation:

  • Problème: convertissez 65,24 kilogrammes en grammes.
  • 1 kilogramme = 1000 grammes. Comptez le nombre de zéros, il y en a trois. Par conséquent, vous devez multiplier par 10 trois fois ou vous pouvez déplacer la virgule vers la droite trois fois.
  • 65,24 x 10 = 652,4 (multiplié une fois)
  • 652,4 x 10 = 6524 (deux fois)
  • 6524 x 10 = 65240 (trois fois)
  • La réponse est 65240 grammes.

  

  Étape 5. Entraînez-vous avec des questions plus difficiles

  Vous trouverez cela plus difficile lorsque vous convertirez des unités préfixées en d'autres unités préfixées. Le moyen le plus simple de résoudre ce problème est de convertir d'abord les unités de base (sans le préfixe), puis de les convertir dans les unités souhaitées. Par exemple:

  • Problème: convertir 793 millilitres en décallitres.
  • S'il y a trois zéros, déplacez la virgule vers la gauche trois fois. (Rappelez-vous, déplacez le point vers la gauche lors de la division.)
  • 793 millilitres = 0,793 litre
  • 10 litres = 1 décalitre puis 1 litre = 0,1 décalitre. Il y a un zéro donc déplacez la virgule vers la gauche une fois.
  • 0,793 litre = 0,0793 décallitre.

  

  Étape 6. Vérifiez vos réponses

  L'erreur qui est souvent commise est de multiplier et de diviser, ou vice versa. Lorsque vous avez votre réponse finale, vérifiez le résultat de la réponse:

  • Si vous convertissez en unités plus grandes, votre nombre devrait être plus petit (comme lors de la conversion de 12 pouces en 1 pied).
  • Si vous convertissez en unités plus petites, votre nombre devrait être plus grand (comme lors de la conversion de 1 pied en 12 pouces).
  • Si les résultats ne correspondent pas à cette réponse, vérifiez votre flux de travail.