- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:27.
- Dernière modifié 2025-01-23 12:18.
La vitesse est un calcul de la vitesse à laquelle quelque chose se déplace à un moment donné. Si vous avez déjà regardé le compteur de vitesse d'une voiture en mouvement, vous verrez le compte de vitesse - plus l'aiguille se déplace loin, plus la vitesse du véhicule est élevée. Il existe plusieurs façons de calculer la vitesse, selon le type d'informations dont vous disposez. En général, la formule vitesse = distance/temps (ou k = j/w) est le moyen le plus simple de calculer la vitesse.
Étape
Méthode 1 sur 3: Utilisation de formules de calcul de vitesse standard

Étape 1. Trouvez la distance qu'un objet a parcourue
La formule de base que la plupart des gens utilisent pour trouver la vitesse de quelque chose est très facile à utiliser. Tout d'abord, vous devez savoir « combien de distance l'objet mesuré a-t-il parcouru ». En d'autres termes, quelle est la distance entre le point de départ et le point d'arrivée de l'objet ?
Cette formule est plus facile à comprendre à travers un exemple. Disons que nous voyageons en voiture jusqu'à une aire de jeux pour "161 kilomètres". En quelques étapes, nous pouvons utiliser ces informations pour terminer le calcul de la formule

Étape 2. Trouvez le temps qu'il faut à l'objet pour parcourir cette distance
La prochaine information dont vous avez besoin est le temps qu'il faut à l'objet pour atteindre une certaine distance. En d'autres termes, combien de temps faut-il à l'objet pour se déplacer du point de départ au point d'arrivée ?
Dans cet exemple, disons que l'objet prend env. deux heures pour arriver à destination.

Étape 3. Divisez la distance par le temps nécessaire pour trouver la vitesse de l'objet
Vous n'avez besoin que de ces deux informations pour connaître la vitesse de l'objet. La distance au temps est égale à la vitesse de l'objet.
Dans cet exemple, 161 kilomètres/2 heures = 80,5 kilomètres/heure.

Étape 4. N'oubliez pas l'unité utilisée
Il est très important d'utiliser les bonnes unités dans votre réponse (comme les kilomètres par heure, etc.) Sans ces unités, il est très difficile pour les gens de comprendre le sens de votre réponse. Vous pouvez également perdre des points si vous utilisez la mauvaise unité lorsque vous faites des devoirs à l'école.
L'unité de vitesse est unité de distance en unité de temps. Par exemple, puisque nous mesurons la distance en kilomètres et le temps en heures, les unités utilisées sont kilomètres/heure (ou kilomètres par heure).
Méthode 2 sur 3: Résolution de calculs plus difficiles

Étape 1. Trouvez plusieurs variables différentes pour résoudre le problème de la distance et du temps
Une fois que vous avez compris la formule de base de la vitesse, vous pouvez l'utiliser pour effectuer des calculs autres que la vitesse. Par exemple, si au début vous ne connaissez que la vitesse de l'objet et une autre variable, vous pouvez réorganiser la formule ci-dessus pour trouver les informations inconnues.
-
Par exemple, disons que nous savons qu'un train roule à 20 kilomètres à l'heure pendant quatre heures, mais nous ne savons pas quelle distance il a parcourue. Pour le savoir, on peut réarranger la formule de la manière suivante:
-
- vitesse = distance/temps
- vitesse × temps = (distance/temps) × temps
- vitesse × temps = distance
- 20 km/heure × 4 heures = distance = 80 kilomètres
-

Étape 2. Convertissez les unités que vous utilisez selon vos besoins
Parfois, vous pouvez calculer la vitesse en utilisant une certaine unité, mais devez la convertir en une autre unité. Dans ce cas, vous devez utiliser un facteur de conversion pour obtenir la réponse selon les bonnes unités. Pour ce faire, écrivez simplement la relation entre les unités sous forme de fraction et multipliez. Lors de la multiplication, inversez la fraction au besoin pour supprimer les unités indésirables. Cette méthode est bien plus simple qu'il n'y paraît !
-
Par exemple, disons que dans l'exemple de problème ci-dessus, nous avons besoin de la réponse en miles au lieu de kilomètres. Un mile équivaut à environ 1,6 kilomètre. Ainsi, nous pouvons faire la conversion comme suit:
-
- 80 kilomètres × 1 mile/1,6 kilomètres = 50 milles
-
- N'oubliez pas que, comme les kilomètres apparaissent au bas de la fraction, cela supprime des kilomètres de la réponse précédente, donc le résultat final utilise des miles.
- Ce site Web fournit des fonctionnalités de conversion pour la plupart des unités couramment utilisées.

Étape 3. Remplacez la variable "distance" par la formule de distance si nécessaire
Les objets ne se déplacent pas toujours selon une trajectoire droite et lisse. Si cela est vrai, vous ne pourrez peut-être pas simplement entrer une valeur numérique comme unité de distance dans la formule de vitesse standard. Cependant, vous devrez peut-être remplacer la lettre j dans la formule k = j/w par une formule qui ressemble à la distance parcourue par l'objet.
-
Par exemple, disons qu'un avion effectue 5 rotations dans les airs sur une distance de 20 milles. L'avion a terminé le tour en une demi-heure. Dans cet exemple, nous devons encore trouver la distance totale parcourue par l'avion avant de pouvoir déterminer sa vitesse. Nous pouvons utiliser la formule pour calculer la distance autour d'un cercle (distance autour de lui) au lieu de j dans cette formule. Cette formule est circonférence = 2πr où r = rayon du cercle. Voici comment le résoudre:
-
- k = (2 × × r)/w
- k = (2 × 10)/0,5
- k = 62,83/0,5 = 125,66 milles/heure
-

Étape 4. Comprenez que k = j/w donne la vitesse moyenne
La formule facile et simple que nous utilisons pour trouver la vitesse a un inconvénient. La valeur résultante est techniquement la vitesse moyenne. Cela signifie que la formule suppose que l'objet que vous mesurez utilise la même vitesse lorsqu'il se déplace. Comme nous le verrons ci-dessous, trouver la vitesse d'un objet en un seul instant sera beaucoup plus difficile.
Pour illustrer cette différence, imaginez la dernière fois que vous avez voyagé en voiture. Il est peu probable que vous voyagiez à la même vitesse que vous voyagez. Cependant, vous commencerez généralement votre voyage à basse vitesse et augmenterez progressivement votre vitesse en cours de route, en vous arrêtant à cause des feux rouges, des embouteillages, etc. Si vous utilisez la formule de vitesse standard pour trouver la vitesse pendant le déplacement, les modifications apportées à cette vitesse ne peuvent pas être détectées. Cependant, vous obtiendrez une réponse qui montre la vitesse moyenne de toutes les différences de vitesse que vous parcourez
Méthode 3 sur 3: Calcul de la vitesse instantanée
Noter:
Cette section utilise des techniques qui sont moins familières aux personnes qui n'ont jamais étudié le calcul. Lisez nos articles sur le calcul pour obtenir de l'aide.
Étape 1. Comprenez que la vitesse est définie comme le taux d'accélération
Les calculs de vitesse de haut niveau sont assez déroutants car les mathématiciens et les scientifiques utilisent des définitions différentes pour décrire la "vitesse" et "l'accélération". L'accélération a deux composantes: un « taux » et une « direction ». Le taux est égal à la vitesse de l'objet. Un changement de direction entraînera un changement d'accélération, mais pas un changement de vitesse.
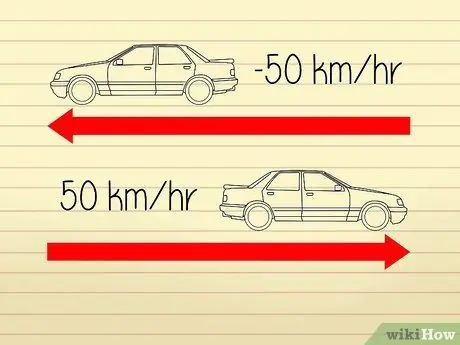
- Par exemple, disons que deux voitures se déplacent dans des directions opposées. Les compteurs de vitesse des deux voitures affichent un chiffre de 50 km/h, ils roulent donc tous les deux à la même vitesse. Cependant, comme les voitures s'éloignent les unes des autres, on peut dire que l'une des voitures a une « accélération » de -50 km/h tandis que l'autre a une « accélération » de 50 km/h.
- Tout comme les calculs de vitesse instantanée, vous pouvez également effectuer des calculs d'accélération instantanée.

Étape 2. Utilisez des valeurs absolues pour mesurer l'accélération négative
Un objet peut avoir un taux d'accélération négatif (s'il se déplace dans une direction négative par rapport à un autre objet). Cependant, il n'y a pas de vitesse négative. Ainsi, dans ce cas, la valeur absolue du taux indique la vitesse de l'objet.
Pour cette raison, dans l'exemple de problème ci-dessus, les deux voitures ont une vitesse de 50km/h.
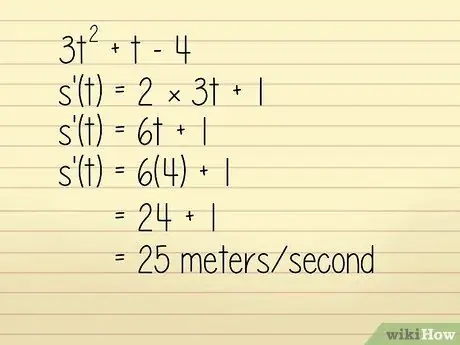
Étape 3. Prenez la dérivée de la position de la fonction
Si vous avez une fonction k(w) qui montre la position d'un objet sans avoir besoin de calculer le temps, la dérivée de k(w) montrera l'accélération sans avoir besoin de chronométrage. Il suffit de brancher la valeur de temps dans cette formule pour que la variable w (ou toute autre valeur de temps utilisée) soit accélérée en fonction de ce temps. De là, vous pouvez facilement trouver la vitesse de l'objet.
-
Par exemple, disons que la position d'un objet dans un mètre est décrite dans l'équation 3q2 + w - 4 où w = temps en secondes. Nous voulons connaître la vitesse de l'objet à w = 4 secondes. Dans ce cas, vous pouvez le résoudre en:
-
- 3w2 +w - 4
- k'(w) = 2 × 3w + 1
- k'(w) = 6w + 1
-
-
Maintenant, nous entrons w = 4:
-
- k'(w) = 6(4) + 1 = 24 + 1 = 25 mètres/seconde. Techniquement, il s'agit d'un calcul d'accélération, mais comme il est positif et que la direction n'est pas mentionnée dans la question, nous pouvons l'utiliser pour trouver la vitesse.
-

Étape 4. Prenez la fonction d'accélération intégrale
L'accélération est un moyen de mesurer la variation de l'accélération d'un objet au fil du temps. Ce sujet est trop complexe pour être entièrement expliqué dans cet article. Cependant, il est utile de noter que lorsque vous avez une fonction a(w) qui représente l'accélération par rapport au temps, l'intégrale de a(w) renverra le résultat de l'accélération basée sur ce temps. N'oubliez pas qu'il est très utile de connaître l'accélération initiale d'un objet afin de pouvoir définir la constante de ce résultat à partir d'une intégrale infinie.
-
Par exemple, disons qu'un objet a une accélération constante (en m/s2 en raison de a(w) = -30. Dites aussi que l'objet a une accélération initiale de 10 m/s. Nous devons trouver la vitesse à w = 12 secondes. Dans ce cas, nous pouvons le résoudre en:
-
- a(w) = -30
- p(w)= a(w)dw = -30dw = -30w + C
-
-
Pour trouver C, nous allons résoudre p(w) pour w = 0. Rappelez-vous que l'accélération initiale de l'objet est de 10 m/s.
-
- p(0) = 10 = -30(0) + C
- 10 = C, donc p(w) = -30w + 10
-
-
Maintenant, nous pouvons entrer w = 12 secondes.
-
- p(12) = -30(12) + 10 = -360 + 10 = -350. Puisque la vitesse est une valeur absolue de l'accélération, la vitesse de l'objet est 350 mètres/seconde.
-
Des astuces
- La pratique, c'est génial ! Essayez de créer votre propre question en remplaçant les nombres dans l'exemple de problème ci-dessus.
- Si vous cherchez un moyen rapide de pratiquer le calcul pour une meilleure vitesse de calcul, utilisez la calculatrice de dérivée en ligne ici et la calculatrice intégrale en ligne ici.






