- Auteur Jason Gerald [email protected].
- Public 2023-12-16 11:11.
- Dernière modifié 2025-06-01 06:06.
Le système de nombres décimaux (base dix) a dix valeurs possibles (0, 1, 2, 3, 4, 5, 6, 7, 8 ou 9) pour chaque position numérique. En revanche, le système numérique binaire (base deux) n'a que deux valeurs possibles représentées par 0 et 1 pour chaque position numérique. Étant donné que le système de nombres binaires est le langage interne des ordinateurs électroniques, les programmeurs informatiques sérieux savent comment passer du système de nombres décimal au système de nombres binaires. Suivez ces étapes simples et également comment maîtriser cette conversion.
Étape
Méthode 1 sur 2: Division courte par deux avec reste

Étape 1. Déterminez le problème
Pour cet exemple, convertissons le nombre décimal 15610 être un nombre binaire. Écrivez le nombre décimal comme nombre à diviser dans le symbole de division inversée. Écrivez la base du système de numérotation de destination (dans cet exemple « 2 » pour binaire) comme diviseur hors courbe du symbole de division.
- Cette méthode est beaucoup plus facile à comprendre lorsqu'elle est dessinée sur papier, et beaucoup plus facile pour les débutants, car elle ne divise que par deux.
- Pour éviter toute confusion avant et après la conversion, notez le numéro de base du système numérique que vous calculez en indice (minuscule écrit sous les lettres normales comme signe distinctif) pour chaque numéro. Dans cet exemple, le nombre décimal aura un indice de 10 et le nombre binaire aura un indice de 2.

Étape 2. Faites la division
Écrivez la réponse entière (quotient) sous le symbole de division longue et écrivez le reste (0 ou 1) à droite du nombre divisé.
Parce que nous divisons par deux, lorsque le nombre divisé est un nombre pair, le reste est 0, et lorsque le nombre divisé est un nombre impair, le reste est 1

Étape 3. Continuez à diviser jusqu'à ce qu'il atteigne zéro
Continuez à descendre, en divisant chaque nouveau quotient par deux et en écrivant le reste à droite de chaque nombre divisé. Arrêtez-vous lorsque le quotient est nul.

Étape 4. Notez le nouveau nombre binaire
En commençant par le plus petit nombre restant, lisez l'ordre du reste dans l'ordre croissant vers le haut. Dans cet exemple, vous devriez obtenir le résultat 10011100. C'est l'équivalent binaire du nombre décimal 156. Ou, s'il est écrit avec son indice de base numérique: 15610 = 100111002.
Cette méthode peut être modifiée pour convertir de la base décimale à n'importe quelle base numérique. Le diviseur est 2 car la base du système de numérotation de destination est la base 2 (binaire). Si la base du système de numérotation de destination est une autre base, remplacez le numéro de base 2 dans cette méthode par le numéro de base approprié. Par exemple, si la base de destination est la base 9, remplacez le numéro de base 2 par 9. Le résultat final sera directement sous la forme du numéro de base de destination
Méthode 2 sur 2: Dérivation de la puissance de deux et de la soustraction

Étape 1. Commencez par créer une table
Notez les puissances des deux nombres de base dans la "base du tableau 2" de droite à gauche. Commencer à 20, écrivez-le comme « 1 ». Augmentez le rang de 1 pour chaque rang. Complétez le tableau jusqu'à ce que vous obteniez un nombre qui se rapproche le plus du nombre du système de nombres décimaux que vous calculez. Pour cet exemple, convertissons le nombre décimal 15610 être un nombre binaire.

Étape 2. Trouvez le nombre avec la plus grande puissance du nombre de base 2
Dans le tableau, choisissez le plus grand nombre égal ou inférieur au nombre à convertir. Le nombre 128 est le nombre avec la plus grande puissance du nombre de base 2 et est également plus petit que 156, alors écrivez un nombre "1" sous cette case dans le tableau, où le plus grand nombre du tableau est à gauche (voir tableau dans l'image ci-dessus). Soustrayez ensuite 128 du nombre initial, vous obtiendrez: 156 - 128 = 28.
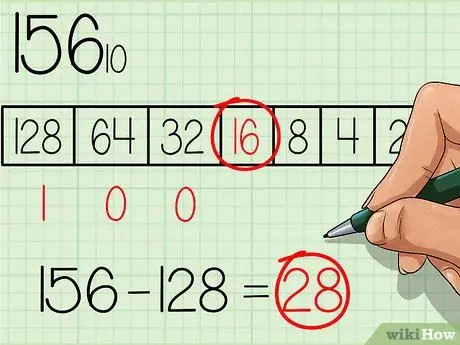
Étape 3. Passez à la puissance inférieure suivante dans le tableau
À l'aide du nouveau numéro (28), continuez dans le tableau de gauche à droite tout en vérifiant si les numéros sont égaux ou inférieurs au nouveau numéro. Le nombre 64 n'est pas inférieur à 28, alors écrivez le nombre « 0 » sous la case 64. Continuez jusqu'à ce que vous trouviez un nombre égal ou inférieur à 28.
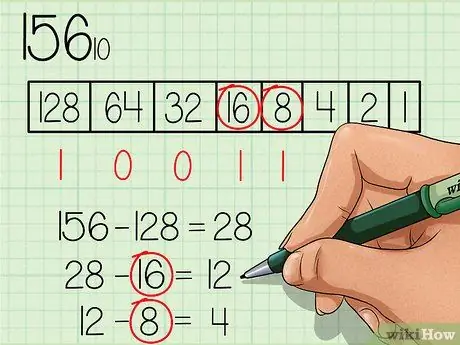
Étape 4. Soustrayez en continu chaque nombre égal ou inférieur au nouveau nombre et marquez le nombre « 1 » sous la case correspondant au nombre approprié
Le nombre 16 est inférieur à 28, alors écrivez le nombre "1" sous la case numérique 16 et soustrayez 16 de 28, vous obtenez ainsi un nouveau nombre 12. Le nombre 8 est inférieur à 12, alors écrivez le nombre "1" sous la case numéro 8 et soustrayez 8 de 12 pour obtenir le nouveau numéro 4.

Étape 5. Continuez jusqu'à ce que vous atteigniez la fin de la table
N'oubliez pas de marquer un « 1 » sous chaque case pour les nombres qui sont égaux ou inférieurs au nouveau nombre, et un « 0 » sous chaque case pour les nombres qui sont encore supérieurs au nouveau nombre.
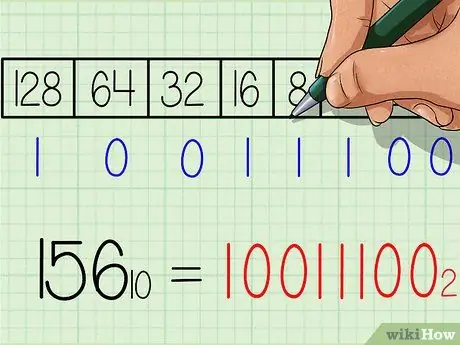
Étape 6. Écrivez la réponse pour le nombre binaire
Le nombre sera exactement le même de gauche à droite que la rangée de nombres « 1 » et « 0 » au bas du tableau. Vous devriez obtenir le résultat 10011100. C'est l'équivalent binaire du nombre décimal 156. Ou lorsqu'il est écrit avec un indice: 15610 = 100111002.
Répéter cette méthode peut vous aider à vous souvenir des pouvoirs de la base deux, vous pouvez donc ignorer l'étape 1
Des astuces
- Le programme Calculator intégré au système d'exploitation peut effectuer cette conversion pour vous, mais en tant que programmeur, il est préférable de commencer par une bonne compréhension du fonctionnement des conversions. Les options de conversion du programme Calculatrice peuvent être rendues visibles en ouvrant le menu « Affichage » et en sélectionnant « Programmeur » (pour Windows 7 et 8).
- La conversion dans la direction opposée, c'est-à-dire du système binaire au système décimal, est généralement plus facile à apprendre en premier.
- Pratiquez souvent la conversion de nombres décimaux en nombres binaires pour devenir plus expert.






