Avec le coefficient de corrélation de rang de Spearman, nous pouvons identifier si deux variables ont une relation de fonction monotone (c'est-à-dire que lorsqu'un nombre augmente, l'autre nombre augmentera également, ou vice versa). Pour calculer le coefficient de corrélation de rang de Spearman, vous devez classer et comparer les ensembles de données pour trouver d2, puis saisissez les données dans la formule de coefficient de corrélation de rang Spearman standard ou simplifiée. Vous pouvez également calculer ces coefficients à l'aide de formules Excel ou de la commande R.
Étape
Méthode 1 sur 3: Manière manuelle
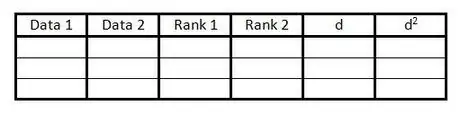
Étape 1. Créez un tableau
Le tableau est utilisé pour inclure toutes les informations nécessaires pour calculer le coefficient de corrélation Spearman Rank. Vous avez besoin d'un tableau comme celui-ci:
- Créez 6 colonnes avec des en-têtes, comme dans l'exemple.
- Préparez autant de lignes vides que le nombre de paires de données.
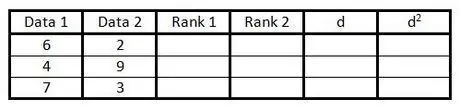
Étape 2. Remplissez les deux premières colonnes avec des paires de données
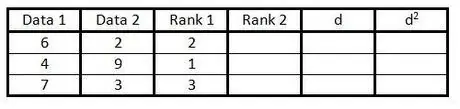
Étape 3. Entrez le classement de la première colonne des groupes de données dans la troisième colonne de 1 à n (nombre de données)
Donnez une note de 1 pour la valeur la plus basse, une note de 2 pour la prochaine valeur la plus basse, et ainsi de suite.
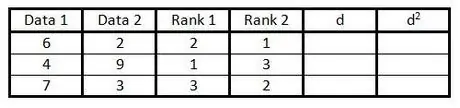
Étape 4. Dans la quatrième colonne, procédez comme à l'étape 3, mais pour classer les données dans la deuxième colonne
-
Moyenne_742 S'il y a deux (ou plus) données qui ont la même valeur, calculez la note moyenne des données, puis saisissez-la dans un tableau en fonction de cette valeur moyenne.
Dans l'exemple de droite, il y a deux valeurs de 5 sur les notes 2 et 3. Puisqu'il y a deux 5, trouvez la moyenne des notes. La moyenne de 2 et 3 est de 2,5, alors entrez une valeur de 2,5 pour les deux valeurs 5.
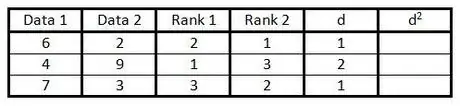
Étape 5. Dans la colonne "d", calculez la différence entre les deux nombres dans la colonne de classement
Autrement dit, si une colonne est classée 1 et l'autre colonne est classée 3, la différence est de 2. (Le signe n'a pas d'importance, car l'étape suivante consiste à mettre la valeur au carré.)
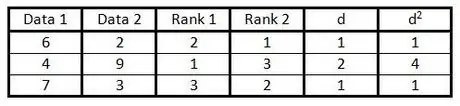
Étape 6. Carré chaque nombre dans la colonne "d" et écrivez le résultat dans la colonne "d2".
Étape 7. Additionnez toutes les données dans la colonne d2".
Le résultat est d2.
Étape 8. Choisissez l'une des formules suivantes:
-
Si aucune des notes n'est la même qu'à l'étape précédente, entrez cette valeur dans la formule simplifiée du coefficient de corrélation de Spearman Rank
Étape8_271 et remplacez "n" par le nombre de paires de données pour obtenir le résultat.
Étape 9_402 -
S'il existe un classement similaire à l'étape précédente, utilisez la formule standard du coefficient de corrélation du classement de Spearman:
Spearman
Étape 9. Interprétez les résultats
La valeur peut varier entre -1 et 1.
- Si la valeur est proche de -1, la corrélation est négative.
- Si la valeur est proche de 0, il n'y a pas de corrélation linéaire.
- Si la valeur est proche de 1, la corrélation est positive.
Méthode 2 sur 3: Utilisation d'Excel
Étape 1. Créez une nouvelle colonne pour les données avec son classement
Par exemple, si vos données se trouvent dans la colonne A2:A11, utilisez la formule "=RANK(A2, A$2:A$11)", et copiez-la jusqu'à ce qu'elle couvre toutes les colonnes et lignes.
Étape 2. Modifiez la même note que celle décrite aux étapes 3 et 4 de la méthode 1
Étape 3. Dans la nouvelle cellule, calculez la corrélation entre les deux colonnes de rang avec la formule "=CORREL(C2:C11, D2:D11)"
Dans cet exemple, C et D font référence à la colonne où se trouve le classement. La nouvelle cellule sera remplie avec la corrélation de rang Spearman.
Méthode 3 sur 3: Utilisation de R
Étape 1. Installez d'abord le programme R si vous ne l'avez pas déjà
(Voir
Étape 2. Enregistrez vos données au format CSV, placez les données que vous souhaitez trouver la corrélation dans les deux premières colonnes
Nous pouvons le faire en utilisant le menu "Enregistrer sous".
Étape 3. Ouvrez l'éditeur R
Si vous travaillez depuis le terminal, exécutez simplement R. Si vous travaillez depuis le bureau, cliquez sur l'icône R.
Étape 4. Tapez la commande suivante:
- d <- read.csv("NAME_OF_YOUR_CSV.csv") et appuyez sur Entrée.
- cast(rang(d[, 1]), rang(d[, 2]))
Des astuces
Les données doivent être constituées d'au moins 5 paires pour que la tendance puisse être vue (le nombre de données est de 3 paires dans l'exemple uniquement pour simplifier les calculs.)
Avertissement
- Le coefficient de corrélation de rang de Spearman identifie uniquement la force de la corrélation lorsque les données augmentent ou diminuent de manière cohérente. S'il y a une autre tendance dans les données, la corrélation de rang de Spearman non fournira une représentation précise.
- Cette formule est basée sur l'hypothèse qu'il n'y a pas d'évaluations égales. Lorsqu'il y a le même rang que dans l'exemple, il faut utiliser cette définition: le coefficient de corrélation du moment de multiplication par rang.
